微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、简答题 如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计粒子所受重力).
(1)在该区域AB边的中点处由静止释放电子,求电子离开ABCD区域的位置;
(2)在电场I区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,求所有释放点的位置;
(3)若将左侧电场II整体水平向右移动L/4,仍使电子从ABCD区域左下角D处离开(D不随电场移动),在电场I区域内由静止释放电子的所有位置.
参考答案:(1)设电子的质量为m,电量为e,在电场I中释放后将做出速度为零的匀加速直线运动,出区域I时的速度为vo,接着进入电场II做类平抛运动,假设电子从CD边射出,出射点纵坐标为y,对电子的整个运动过程运用动能定理和匀变速直线运动公式有:eEL=12mv2,
在电场Ⅱ区域内的偏转,L=vt,y1=12at2=eE2m?L2v2=14L,方向向下,
故:y=L2-y1=L4
所以位置坐标(-2L,14L)
(2)设释放位置坐标为(x,y),在电场I中电子被加速到v1,然后进入电场II做类平抛运动,并从D点离开,有:eEx=12mv2,
L=vt,y?=12at2=eE2m?L2v2=L24x,所以满足xy=L24方程的点即为释放点的位置
(3)设释放位置坐标为(x,y),eEx=12mv2,在电场I中加速到v2,进入电场II后做类平抛运动,在高度为y′处离开电场II时的情景与(2)中类似,然后电子做匀速直线运动,经过D点,则有:
L=vt1,L4=vt2,
y2=12at21=eE2m?L2v2=L24x,
y3=at1t2=eEm?Lv?L4v=eEL24mv2=L28x,
y=y2+y3=L24x+L28x=3L28x,
所以满足y=3L28x方程的点即为释放点的位置.
答:(1)在该区域AB边的中点处由静止释放电子,电子从(-2L,14L)离开ABCD区域.
(2)在电场I区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,所有释放点为满足xy=L24的位置.
(3)若将左侧电场II整体水平向右移动在电场I区域内由静止释放电子的所有位置,在电场I区域内由静止释放电子的所有位置为y=3L28x.
本题解析:
本题难度:一般
2、选择题 关于运动物体所受的合外力、合外力做的功、物体的动能变化三者之间的关系,下列说法正确的是(? )
A.运动物体所受的合外力不为零,合外力必做功,物体的动能肯定要变化
B.运动物体所受的合外力为零,则物体的动能肯定不变
C.运动物体的动能保持不变,则该物体所受合外力一定为零
D.运动物体所受合外力不为零,则该物体一定做变速运动,其动能一定要变化
参考答案:B
本题解析:物体做匀速圆周运动,合外力不为零,但合外力不做功,所以动能不变,ACD错。运动物体所受的合外力为零,因此合外力做功为零,则物体的动能肯定不变,B对。
点评:本题考查了对动能定理的理解,其中匀速圆周运动是其中一个比较特殊的例子。
本题难度:简单
3、选择题 如图所示,有一足够宽的匀强电场,电场强度大小为E,方向竖直向下,在电场中的O点,沿同一水平方向以不同的速率射出若干个带电粒子,它们的质量均为m、带电量均为+q,但速率不等,粒子的重力及相互间的影响不计,若把每个粒子的动能增大到各自初动能3倍的位置分别记为P1、P2、P3、…,则P1、P2、P3、…的连线形状为(? )
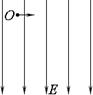
A.一个圆
B.双曲线的一支
C.一条抛物线
D.一条直线
参考答案:D
本题解析:所有带电粒子在电场受力情况相同,均为qE,其方向与初速度方向相垂直,都将做类平抛运动,即在初速度方向(垂直于电场方向做匀速直线运动),在电场方向上做初速度为0的匀加速直线运动,设粒子动能增大到初动能3倍时的速度为v,方向与水平方向的夹角为α,在沿电场方向的分量为vy,所在位置与出射点O的连线与初速度v0方向的夹角为β,粒子沿初速度方向的位移为x,沿电场方向的位移为y,运动时间为t,加速度为a,有:x=v0t,y=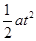 ,vy=at,所以tanβ=
,vy=at,所以tanβ=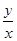 =
=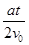 ,其动能变化量为:ΔEk=
,其动能变化量为:ΔEk=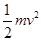 -
-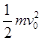 =
=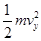 ,所以有:tanα=
,所以有:tanα=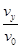 =
= =
=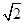 =2tanβ,即P1、P2、P3、…与出射点O的连线与初速度v0方向的夹角相等,即P1、P2、P3、…的连线形状为一条直线,故选项D正确。
=2tanβ,即P1、P2、P3、…与出射点O的连线与初速度v0方向的夹角相等,即P1、P2、P3、…的连线形状为一条直线,故选项D正确。
本题难度:一般
4、选择题 (2011年福建三明统考)如图4-2-6所示,ABCD是一个盆式容器,盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧,BC为水平的,其距离d=0.5 m,盆边缘的高度为h=0.3 m.在A处放一个质量为m的小物块并让其从静止出发下滑.已知盆内侧壁是光滑的,而BC面与小物块间的动摩擦因数为μ=0.1.小物块在盆内来回滑动,最后停下来,则停的地点到B的距离为( )

图4-2-6
A.0.5 m
B.0.25 m
C.0.10 m
D.0
参考答案:D
本题解析:选D.从开始下滑到静止过程,由动能定理得:mgh-μmgs=0解得s=3 m=6d,故距离B点0 m,选项D正确.
本题难度:一般
5、计算题 如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路在滑至C点停止.人与雪橇的总质量为70 kg.表中记录了沿坡滑下过程中的有关数据,请根据图表及图中的数据解决下列问题:(取g="10" m/s2)
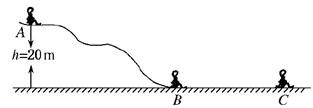
位置
| A
| B
| C
|
速度( m/s)
| 2.0
| 12.0
| 0
|
时间(s)
| 0
| 4
| 10
|
?(1)人与雪橇从A到B的过程中,损失的机械能为多少?
(2)设人与雪橇在BC段所受阻力恒定,求阻力的大小.
(3)人与雪橇从B到C的过程中,运动的距离.
参考答案:(1)9100 J? (2)140 N? (3)36 m
本题解析:(1)从A到B的过程中,人与雪橇损失的机械能为:
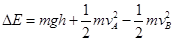 ? ①
? ①
代入数据得:ΔE="9100" J
(2)人与雪橇在BC段做减速运动的加速度:
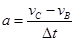 ? ②
? ②
根据牛顿第二定律:Ff=ma? ③
由②③得:Ff="140" N.
(3)由动能定理得: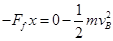
代入数据解得:x="36" m.
本题难度:简单