1、简答题  一小球自A点竖直向上抛出，在大风的情况下，若风力的大小恒定、方向水平向右，小球运动的轨迹如图所示（小球的运动可看作竖直方向的竖直上抛运动和水平方向的初速为零的匀加速度直线运动的合运动）．在小球运动的轨迹上A、B两点处在同一水平线上，M点为轨迹的最高点．小球抛出的初动能为5J，小球在最高点M处的动能为2J，其它的阻力不计．求：
（1）小球水平位移S1与S2之比；
（2）小球的重力G与所受风力F的比值；
（3）小球落回到B点时的动能EKB；
（4）小球从A点到B点的运动过程中，小球动能的最小值．

参考答案：（1）小球在竖直方向上做竖直上抛运动，根据对称性得知，从A点至M点和从M点至B点的时间t相等．
小球在水平方向上做初速为零的匀加速直线运动，设加速度为a，则
? S1=12at2
? S2=12a(2t)2-12at2=32at2
?所以S1S2=13?
（2）由题，12mv2A=5J，得vA=

本题解析：

本题难度：一般

2、简答题  如图所示，光滑绝缘水平面AB与倾角θ=370，长L=6m的绝缘斜面BC在B处圆滑相连，在斜面的C处有一与斜面垂直的弹性绝缘挡板，质量m=0.5kg、所带电荷量q=5x10-5C的绝缘带电滑块置于斜面的中点D，整个空间存在水平向右的匀强电场，场强E=2xlO5N/C，现让滑块以v0=12m/s的速度沿斜面向上运动．设滑块与挡板碰撞前后所带电荷量不变、速度大小不变，滑块和斜面间的动摩擦因数μ=0.1，求：
（1）滑块第一次与挡板碰撞时的速度大小；
（2）滑块第一次与挡板碰撞后能达到左端的最远点离B点的距离；
（3）滑块运动的总路程．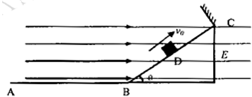

参考答案：（1）滑块从D到C的过程中，根据动能定理可得：
qEcosθ?L2-mgsinθ?L2-Ff?L2=12mv2C-12mv2D?
而滑动摩擦力：Ff=μ（mgcosθ+qEsinθ）?
解得vC=

本题解析：

本题难度：一般

3、选择题  质量为m，带电量为+q的小球从距离地面高为h处以一定的初速度水平抛出，在距抛出点水平距离L处，有一根管口比小球直径略大的竖直细管，管的上口距离地面h/2．为使小球能无碰撞的通过管子，可以在管口上方的整个区域内加上水平方向的匀强电场，如图，则下列说法中正确的是

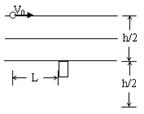
A．所加电场方向应该水平向左
B．小球平抛的水平初速度大小为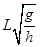
C．所加电场的电场强度为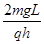
D．小球落地的动能为mgh+

参考答案：AC

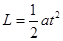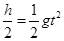本题解析：据题意，要使小球与管子无碰撞，需要使小球到达上管口时水平速度刚好为0，则电场水平向左，使小球在水平方向做匀减速直线运动，有：，而，竖直方向做自由落体运动，有：，可求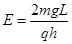：，故A、C选项正确；小球在水平方向做末速度为0的匀减速直线运动，则有：，所以初速度为，故B选项错误；小球从抛出到落地过程中据动能定理有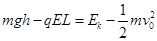：，则小球落地动能为：，故D选项错误。

本题难度：一般

4、选择题  人骑自行车下坡，坡长L=500m，坡高h=8m，人和车的总质量为100kg，下坡时初速度为4m/s，人不踏车的情况下，到达坡底时的车速为10m/s，g=10m/s2,则下坡过程中阻力所做的功为
A.-4000J
B.-5000J
C.-3800J
D.-4200J

参考答案：C

本题解析：试题分析：下坡过程中，重力做正功，阻力做负功，所以根据动能定理可得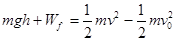：，代入数据可得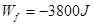，故C正确，ABD错误，
考点：考查了动能定理的应用
点评：在应用动能定理解决问题时，可以不考虑过程，只需要注意始末状态即可，所以动能定理是解决变力做功，多过程问题的首选方法

本题难度：一般

5、计算题  为了研究过山车的原理，某兴趣小组提出了下列设想：取一个与水平方向夹角为37°、长为l=2.0m的粗糙倾斜轨道AB，通过水平轨道BC与竖直圆轨道相连，出口为水平轨道DE，整个轨道除AB段以外都是光滑的。其AB与BC轨道以微小圆弧相接，如图所示。一个小物块以初速度v0＝4.0m/s从某一高处水平抛出，到A点时速度方向恰好沿AB方向，并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数μ=0.50。（g＝10m/s2、sin37°＝0.60、cos37°＝0.80）
（1）求小物块到达A点时速度。
（2）要使小物块不离开轨道，并从轨道DE滑出，求竖直圆弧轨道的半径应该满足什么条件？
（3）为了让小物块不离开轨道，并且能够滑回倾斜轨道AB，则竖直圆轨道的半径应该满足什么条件？

参考答案：解：（1）小物块做平抛运动，经时间t到达A处时，令下落的高度为h，水平分速度v0，竖直速度为vy，小物块恰好沿斜面AB方向滑下，则tan37°=vy/v0
得vy=3 m/s，所以小物块到A点的速度为5m/s
（2）物体落在斜面上后，受到斜面的摩擦力Ff=μFN=μmgcos37°
设物块进入圆轨道到达最高点时有最小速度v1，此时物块受到的重力恰好提供向心力，令此时的半径为 R0，则mg=mv12/R0
物块从抛出到圆轨道最高点的过程中，根据动能定理有：
mg(h+lsin37°－2R0)－μmgcos37°·l = mv12/2－mv02/2
联立上式，解得R0=0.66m
若物块从水平轨道DE滑出，圆弧轨道的半径满足R1≤0.66m
（3）为了让小物块不离开轨道，并且能够滑回倾斜轨道AB，则物块上升的高度须小于或于某个值R，则 mg(h+lsin37°)／μmgcos37°·l－mgR=0－mv02/2
解得R=1.65m
物块能够滑回倾斜轨道AB，则R2≥1.65m

本题解析：

本题难度：困难