|
高考物理题《牛顿第二定律及应用》考点特训(2017年冲刺版)(八)
2017-09-25 08:02:26
来源:91考试网
作者:www.91exam.org 【 大 中 小】
|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 如图,欲使在粗糙斜面上匀速下滑的木块A停下,可采用的方法是( )
A.增大斜面的倾角
B.对木块A施加一个垂直于斜面的力
C.对木块A施加一个竖直向下的力
D.在木块A上再叠放一个重物
| 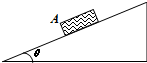
参考答案:A、木块匀速滑下,合力为零,根据平衡条件得 mgsinθ=μmgcosθ;若增大斜面的倾角θ,重力沿斜面向下的分力mgsinθ增大,滑动摩擦力f=μmgcosθ减小,木块的合力方向将沿斜面向下,木块做加速运动.故A错误.
B、对木块A施加一个垂直于斜面的力F,重力沿斜面向下的分力mgsinθ不变,而滑动摩擦力f=μ(F+mgcosθ)增大,合力方向沿斜面向上,木块做减速运动,可以使木块停下.故B正确.
C、对木块A施加一个竖直向下的力,由于(F+mg)sinθ=μ(F+mg)cosθ,木块的合力仍为零,仍做匀速运动,不可能停下.故C错误.
D、由A项分析可知,mgsinθ=μmgcosθ得? sinθ=μcosθ,与质量无关,在木块A上再叠放一个重物后,整体匀速下滑,不可能停下.故D错误.
故选B
本题解析:
本题难度:一般
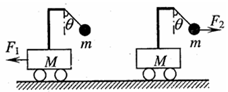
2、选择题 如上右图所示,两个完全相同的小车质量为 ,放在光滑的水平面上,小车横梁上用细线各悬挂一质量为 ,放在光滑的水平面上,小车横梁上用细线各悬挂一质量为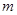 的小球,若分别施加水平恒力 的小球,若分别施加水平恒力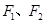 ,整个装置分别以加速度 ,整个装置分别以加速度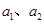 做匀加速运动,但两条细线与竖直方向夹角均为 做匀加速运动,但两条细线与竖直方向夹角均为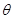 ,则下列判断正确的是: ,则下列判断正确的是:
A.两细线的拉力大小相同
B.地面对两个小车的支持力相同
C.水平恒力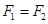
D.两个小车的加速度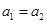
参考答案:AB
本题解析:分析:运用整体法和隔离法,对小球和整体进行分析,求出绳子的拉力、加速度,比较出拉力的大小和加速度大小.再对整体分析,根据牛顿第二定律比较出水平恒力的大小,以及在竖直方向上合力等于零,比较出支持力的大小.
解答:解:先对右图中情况下的整体受力分析,受重力、支持力和拉力
根据牛顿第二定律,有
F2=(M+m)a?①
再对左图中情况下的小球受力分析,如图

根据牛顿第二定律,有
F2-T2sinα=ma2?②
T2cosα-mg=0?③
由以上三式可解得
T2=" Mg/" cosα,a2= mgtanα/M.
再对左图中小球受力分析,如图

由几何关系得
F合=mgtanα?T1= mg/cosα
则a1= mgtanα/m=gtanα
因为m<M,则a1>a2.拉力T1=T2.
对整体分析,F合=(M+m)a,则F1>F2.
在竖直方向上有:N=(M+m)g,所以N1=N2.故A、B正确, C、D错误.
故选A、B.
点评:本题关键要多次对小球和整体受力分析,求出合力,得出加速度和绳子拉力进行比较.
本题难度:一般
3、计算题 如图所示,有一长度L=1 m、质量M=10 kg的平板小车,静止在光滑的水平面上,在小车一端放置一质量m=4 kg的小物块,物块与小车间的动摩擦因数μ=0.25,要使物块在2 s内运动到小车的另一端,求作用在物块上的水平力F是多少?(g取10 m/s2)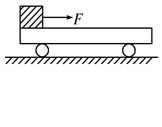
参考答案:16 N
本题解析:由下图中的受力分析,根据牛顿第二定律有

F-Ff=ma物?①
Ff′=Ma车?②
其中Ff=Ff′=μmg?③
由分析图结合运动学公式有x1=a车t2?④
x2=a物t2?⑤
x2-x1=x?⑥
由②③解得a车=1 m/s2?⑦
由④⑤⑥⑦解得a物=1.5 m/s2
所以F=Ff+ma物=m(μg+a物)=4×(0.25×10+1.5) N=16 N.
本题难度:一般
4、计算题 (16分)如图所示,MN、PQ是两根足够长的光滑平行金属导轨,导轨间距为d,导轨所在平面与水平面成θ角,M、P间接阻值为R的电阻。匀强磁场的方向与导轨所在平面垂直,磁感应强度大小为B。质量为m、阻值为r的金属棒放在两导轨上,在平行于导轨的拉力作用下,以速度v匀速向上运动。已知金属棒与导轨始终垂直并且保持良好接触,重力加速度为g。求:
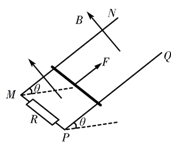
(1)金属棒产生的感应电动势E;
(2)通过电阻R电流I;
(3)拉力F的大小。
参考答案:(1)Bdv;(2)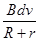 ;(3) ;(3) 。 。
本题解析:(1)根据法拉第电磁感应定律E=Bdv………………………………………4分
(2)根据闭合电路欧姆定律
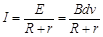 ……………………………………………4分 ……………………………………………4分
(3)导体棒的受力情况如图所示,根据牛顿第二定律有
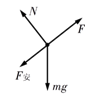
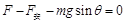
又因为:
所以: ………………………………………8分 ………………………………………8分
本题难度:一般
5、简答题 如图所示,在两条平行的虚线内存在着宽度为L、场强为E的匀强电场,在与右侧虚线相距也为L处有一与电场平行的屏.现有一电荷量为+q、质量为m的带电粒子(重力不计),以垂直于电场线方向的初速度v0射入电场中,v0方向的延长线与屏的交点为O.试求:
(1)粒子在电场中运动的时间;
(2)粒子刚射出电场时的速度方向与初速度方向间夹角的正切值tanα;
(3)粒子打到屏上的点P到O点的距离Y.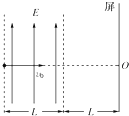
参考答案:(1)粒子在垂直于电场线的方向上做匀速直线运动,则粒子在电场中运动的时间的时间t=Lv0.
(2)设粒子射出电场时沿平行电场线方向的速度为vy,根据牛顿第二定律,粒子在电场中的加速度为:a=qEm
所以vy=at=aLv0=qELmv0
所以粒子刚射出电场时的速度方向与初速度方向间夹角的正切值为tanα=vyv0=qELmv20.
(3)设粒子在电场中的偏转距离为y,则y=12at2=12?qELmv0t2
又Y=y+Ltanα?
解得:Y=3qEL22mv20
答:
(1)粒子在电场中运动的时间是Lv0;
(2)粒子刚射出电场时的速度方向与初速度方向间夹角的正切值tanα为qELmv20;
(3)粒子打到屏上的点P到O点的距离Y是3qEL22mv20.
本题解析:
本题难度:一般
| 