1、计算题  （13分）如图所示，两块平行金属板竖直放置，两板间的电势差U=1.5×103 V（仅在两板间有电场），现将一质量m=1×10-2 kg、电荷量q=4×10-5 C的带电小球从两板的左上方距两板上端的高度h="20" cm的地方以初速度v0="4" m/s水平抛出，小球恰好从左板的上边缘进入电场，在两板间沿直线运动，从右板的下边缘飞出电场，求：

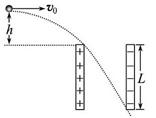
( 1 )进入电场时速度的大小.
（2）金属板的长度L.
（3）小球飞出电场时的动能Ek.

参考答案：（1）v1=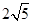?m/s(2)15m(3)0.175 J

本题解析：（1）由动能定理：
v1=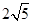?m/s
(2)小球到达左板上边缘时的竖直分速度：
vy= ?="2" m/s
设小球此时速度方向与竖直方向之间的夹角为θ，则：
tanθ=??
小球在电场中沿直线运动，所受合力方向与运动方向相同，
设板间距为d，
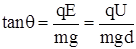则：?
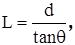
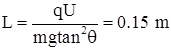解得:?
(3)电场中运动过程
?
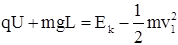解得Ek="0.175" J?
本题考查带电粒子在电场中的偏转，进入电场之前粒子只受重力做功，由动能定理可求得进入电场前的速度大小，进入电场后，根据力的独立作用原理可知竖直方向受到重力作用，竖直分运动为匀加速直线运动，水平方向受到电场力的作用，水平方向做匀变速直线运动，先把进入电场速度分解为水平和竖直方向，粒子从右端飞出，再由两个分运动公式求解

本题难度：一般

2、计算题  如图所示，边长为L的正方形区域abcd内存在着匀强电场。电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场，不计带电粒子的重力。
(1)若粒子从c点离开电场，求粒子离开电场时的动能Ek1。
(2)若粒子离开电场时动能为Ek"，则电场强度可能为多大？

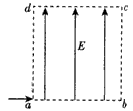
参考答案：解：(1)L=v0t

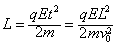
qEL=Ek1-Ek，所以Ek1=qEL+Ek=5Ek
(2)若粒子由bc边离开电场，L=v0t，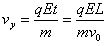

所以
若粒子由cd边离开电场，qEL=Ek"- Ek
所以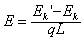

本题解析：

本题难度：困难

3、选择题  如图6－3－12所示，A、B为平行金属板，两板相距为d，分别与电源两极相连，两板的中央各有一小孔M和N.今有一带电质点，自A板上方相距为d的P点由静止自由下落(P、M、N在同一竖直线上)，空气阻力忽略不计，到达N孔时速度恰好为零，然后沿原路返回．若保持两极板间的电压不变，则错误的说法是(　　)

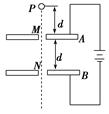
图6－3－12
A．把A板向上平移一小段距离，质点自P点自由下落后仍能返回
B．把A板向下平移一小段距离，质点自P点自由下落后将穿过N孔继续下落
C．把B板向上平移一小段距离，质点自P点自由下落后仍能返回
D．把B板向下平移一小段距离，质点自P点自由下落后将穿过N孔继续下落

参考答案：B

本题解析：选B.电容器两极板间电压U保持不变．若质点P运动到N孔，速度为零，重力做功与电场力做功相等，则不论A板上移还是下移，重力做功都与电场力做功相等，质点均能沿原路返回．若把B板向上平移一小段距离，重力做功变小，电场力做功不变，因此质点可以原路返回．若把B板向下平移一小段距离，质点到达N孔后有一竖直向下的速度，即将穿过N孔继续下落．

本题难度：一般

4、选择题  如图所示，在两块带电平行金属板间，有一束电子沿Ox轴方向射入电场，在电场中的运动轨迹为OCD。已知2OA=AB，则电子在OC段和CD段动能的增加量之比△EkC：△EkD为

[? ]
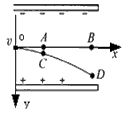
A、1：2
B、1：3
C、1：8
D、1：9

参考答案：C

本题解析：

本题难度：一般

5、计算题  （12分）如图所示，在铅板A上有一个发射源C，可向各个方向射出速率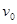=2.8×106m/s的电子，B为金属网，A、B连接在电路上，电源电动势E=20V，内阻不计，滑动变阻器范围为0~20Ω， A、B间距d=10cm，M为荧光屏(足够大)，它紧挨着金属网外侧，已知电子的比荷，现将图中滑动变阻器滑片
置于Rap=5.6Ω，闭合开关后，求：

⑴ A、B间场强大小；
⑵ 不同方向射出的电子到达荧光屏的时间不同，则电子到达
荧光屏的最长时间和电子到达荧光屏范围的最大宽度是多少；
⑶ 调节R使粒子打在荧光屏上面积范围缩小为原来一半，
此时调节Rap至多大？

参考答案：（1）56V/m（2）0.8m（3）11.2Ω

本题解析：（1）设滑动变阻器最大阻值为R0，有? 2分
（2）平行板射出的电子，运动时间最长，有
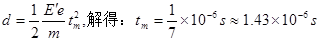? 4分
荧光屏范围的最大宽度：? 2分
（3）荧光屏范围面积为：
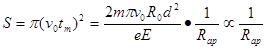? 2分
所以，，有? 2分
本题考查带电粒子在电场中的偏转，电容器两端电压为滑动变阻器左半部分两端电压，所以当划片滑到最右端时极板电压最大，由Ｅ＝Ｕ／ｄ可求得场强大小，平行板射出的电子，运动时间最长，在水平方向电场力提供加速度做匀加速直线运动，由运动学公式可求得运动时间大小，沿竖直方向发射的电子打在范围的边缘处，由类平抛运动可求得竖直位移大小，再由面积公式可求得范围面积

本题难度：简单