微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 (15分)如图所示的空间,匀强电场的方向竖直向下,场强为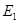 ,匀强磁场的方向水平向外,磁感应强度为
,匀强磁场的方向水平向外,磁感应强度为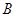 .有两个带电小球A和B都能在垂直于磁场方向的同一竖直平面内做匀速圆周运动(两小球间的库仑力可忽略),运动轨迹如图。已知两个带电小球A和B的质量关系为
.有两个带电小球A和B都能在垂直于磁场方向的同一竖直平面内做匀速圆周运动(两小球间的库仑力可忽略),运动轨迹如图。已知两个带电小球A和B的质量关系为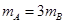 ,轨道半径为
,轨道半径为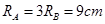 .
.
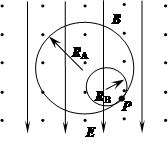
(1)试说明小球A和B带什么电,它们所带的电荷量之比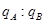 等于多少?
等于多少?
(2)指出小球A和B的绕行方向?
(3)设带电小球A和B在图示位置P处相碰撞,且碰撞后原先在小圆轨道上运动的带电小球B恰好能沿大圆轨道运动,求带电小球A碰撞后所做圆周运动的轨道半径(设碰撞时两个带电小球间电荷量不转移)。
参考答案:(1)两小球都带负电荷,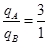 ?(2)两带电小球的绕行方向都相同?(3)
?(2)两带电小球的绕行方向都相同?(3)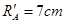
本题解析:
试题分析: (1)因为两带电小球都在复合场中做匀速圆周运动,故必有 ,由电场方向可知,两小球都带负电荷?(2分)
,由电场方向可知,两小球都带负电荷?(2分)
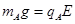
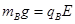 ?(1分)
?(1分)
且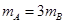
可得: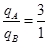 ?(2分)
?(2分)
(2)由题意可知,两带电小球的绕行方向都相同
由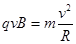 ?(2分)
?(2分)
得: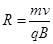
由题意有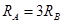 ?(1分)
?(1分)
解得: ?(2分)
?(2分)
(3)由于两带电小球在P处相碰,切向合外力为零,故两带电小球在相碰处的切向动量守恒,
有: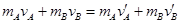 ?(2分)
?(2分)
解得: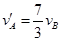 ?
?
而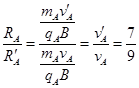 ?(1分)
?(1分)
所以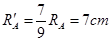 ?(2分)
?(2分)
本题难度:一般
2、简答题 如图所示,在水平桌面上做匀速运动的两个小球,质量分别为m1和m2,沿着同一直线向相同的方向运动,速度分别为V1和V2,当第二个小球追上第一个小球时两球相碰,碰后的速度分别为V1′和V2′,试根据牛顿运动定律和运动学公式证明两球碰撞前的动量之和等于碰撞后的动量之和.

参考答案:证明:根据牛顿第二定律,碰撞过程中两球的加速度分别是:
a1=F1m1 a2=F2m2
根据牛顿第三定律F1与F2大小相等,方向相反,即:
F1=-F2
所以有:m1a1=-m2a2
碰撞时两球之间力的作用时间很短,用△t表示.这样,加速度与碰撞前后速度的关系就是:
a1=v′1-v1△t a2=v′2-v2△t
把加速度的表达式代人 m1a1=-m2a2移项后得到:
m1v1+m2v2=m1v′1+m2v′2
即可证:两球碰撞前的动量之和等于碰撞后的动量之和.
答:根据牛顿运动定律和运动学公式证明两球碰撞前的动量之和等于碰撞后的动量之和见上.
本题解析:
本题难度:一般
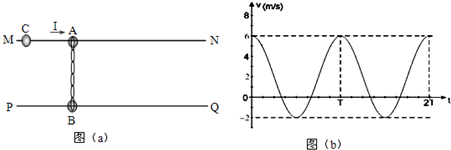
3、简答题 水平固定的两根足够长的平行光滑杆MN、PQ,两者之间的间距为L,两光滑杆上分别穿有一个质量分别为MA=0.1kg和MB=0.2kg的小球A、B,两小球之间用一根自然长度也为L的轻质橡皮绳相连接,开始时两小球处于静止状态,轻质橡皮绳处于自然伸长状态,如图(a)所示.现给小球A一沿杆向右的水平瞬时冲量I,以向右为速度正方向,得到A球的速度-时间图象如图(b)所示.(以小球A获得瞬时冲量开始计时,以后的运动中橡皮绳的伸长均不超过其弹性限度.)
(1)求瞬时冲量I的大小;
(2)在图(b)中大致画出B球的速度-时间图象;
(3)若在A球的左侧较远处还有另一质量为MC=0.1kg小球C,某一时刻给C球4m/s的速度向右匀速运动,它将遇到小球A,并与之结合在一起运动,试定量分析在各种可能的情况下橡皮绳的最大弹性势能.
参考答案:
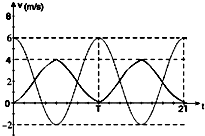
(1)由图象得VA=6m/s,
又I=MAVA-0=0.6N.m
(2)B的速度-时间图象如图
MAVA=(MA+MB)V1
?V1=2m/s
MAVA=MAVA′+MBV2?
?解得V2=4m/s
(3)因A、B、C三小球水平方向系统不受外力,故动量守恒.
由此可得:不论A、C两球何时何处相互作用,三球相互作用的过程中三球具有的共同速度是一个定值,即三球速度相同时的总动能是一定值.
MAVA+MCVC=(MA+MB+MC)V共?
解得V共=2.5m/s
当三球速度相同时橡皮绳子弹性势能最大,所以当A球在运动过程中速度减为4m/s与C球同向时,C球与之相碰时系统损失能量最小(为0),此情况下三球在运动过程中橡皮绳具有的最大弹性势能为EPM1
EPM1=12MAVA2+12MCVC2-12(MA+MB+MC)V共2=1.35J
当A球在运动过程中速度为2m/s与C球反向时,C球与之相碰时系统损失能量最大,此情况下三球运动的过程中橡皮绳具有的最大弹性势能为EPM2
MCVC-MAVA=(MA+MC)V3
解得V3=1m/s
EPM2=12(MA+MC)V32+12MBV22-12(MA+MB+MC)V共2=0.45J
由上可得:橡皮绳具有的最大弹性势能EPM的可能值在0.45J-1.35J的范围内.
答:(1)瞬时冲量I的大小为0.6N.m.
(2)如图所示.
(3)橡皮绳具有的最大弹性势能EPM的可能值在0.45J-1.35J的范围内.
本题解析:
本题难度:一般
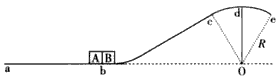
4、计算题 如图所示,一条轨道固定在竖直平面内,粗糙的ab段水平,bcde段光滑,cde段是以O为圆心、R为半径的一小段圆弧。可视为质点的物块A和B紧靠在一起,静止于b处,A的质量是B的3倍。两物块在足够大的内力作用下突然分离,分别向左、右始终沿轨道运动。B到d点时速度沿水平方向,此时轨道对B的支持力大小等于B所受重力的3/4,A与ab段的动摩擦因数为μ,重力加速度g,求:
(1)物块B在d点的速度大小;
(2)物块A滑行的距离s。
参考答案:解:(1)B在d点,根据牛顿第二定律有:
解得: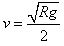
(2)B从b到d过程,只有重力做功,机械能守恒有: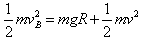 ? ①
? ①
AB分离过程动量守恒有: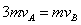 ? ②
? ②
A匀减速直线运动,用动能定理得: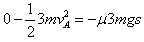 ? ③
? ③
联立①②③,解得: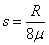
本题解析:
本题难度:一般
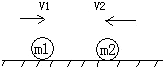
5、简答题 如图示,质量为m1=1kg和m2=2kg的两个小球在光滑的水平面上分别以V1=2m/s和V2=0.5m/s的速度相向运动,某时刻两球发生碰撞,碰后m1以1m/s的速度被反向弹回,求:
①碰后m2的速度;
②两球发生碰撞的过程中m1受到的冲量.
参考答案:①以两球组成的系统为研究对象,以m2的初速度方向为正方向,
由动量守恒定律得:m2v2-m1v1=m1v1′+m2v2′,解得:v2′=-1m/s,方向向右;
②以向右为正方向,两球碰撞过程,对m1,由动量定理得:
I=m1v1′-m1v1=1×1-1×2=-1kg?m/s,方向向左;
答:①碰后m2的速度大小为1m/s,方向向右;
②两球发生碰撞的过程中m1受到的冲量大小为1kg?m/s,方向向左.
本题解析:
本题难度:一般