1、计算题  如图所示，光滑水平面轨道上有三个木块A、B、C，质量分别为mB=mC=2m，mA=m，A、B用细绳连接，中间有一压缩的弹簧（弹簧与滑块不栓接）。开始时A、B以共同速度v0运动，C静止。某时刻细绳突然断开，A、B被弹开，然后B又与C发生碰撞并粘在一起，最终三滑块速度恰好相同。求B与C碰撞前B的速度。

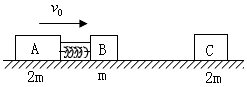
参考答案：解：设共同速度为v，球A和B分开后，B的速度为vB，由动量守恒定律有


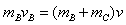
联立这两式得B和C碰撞前B的速度为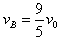

本题解析：

本题难度：一般

2、选择题  有一种硬气功表演，表演者平卧在地面，将一大石板置于他的身体上，另一个人将重锤举到高出并砸向石板，石板被砸碎，而表演者却安然无恙。假设重锤与石板撞击后二者具有相同的速度。表演者在表演时尽量挑选质量较大的石板。对这一现象，下面的说法正确的是
A．重锤在与石板撞击的过程中，重锤与石板的总机械能守恒
B．石板的质量越大，石板获得动量就越小
C．石板的质量越大，石板所受到的打击力就越小
D．石板的质量越大，石板获得的速度就越小

参考答案：D

本题解析：抽象为碰撞模型，碰撞中满足动量守恒定律、重锤的动能大于碰后重锤和石板的总动能，碰撞后两者速度相同属于能量损失最大的一类碰撞，A错误；石板质量越大，共同速度越小，重锤的动量损失越多，则石板获得的动量就越大，B错误、D正确；表演者挑选质量较大的石板，在打击时产生更大的打击力，石板就越容易砸碎，C错误。

本题难度：简单

3、计算题  某同学用一个光滑的半圆形轨道和若干个大小相等、可视为质点的小球做了三个有趣的实验，轨道固定在竖直平面内，且两端同高。第一次，他将一个小球从离轨道最低点的竖直高度h处由静止沿轨道下滑（h远小于轨道半径），用秒表测得小球在轨道底部做往复运动的周期为T；第二次，他将小球A放在轨道的最低点，使另一个小球B从轨道最高点由静止沿轨道滑下并与底部的小球碰撞，结果小球B返回到原来高度的1/4，小球A也上滑到同样的高度；第三次，用三个质量之比为m1:m2:m3＝5:3:2的小球做实验，如图所示，先将球m2和m3放在轨道的最低点，球m1从某一高度由静止沿轨道下滑，它们碰后上升的最大高度分别为h1、h2和h3，不考虑之后的碰撞。设实验中小球间的碰撞均无能量损失。重力加速度为g。求：
（1）半圆形轨道的半径R；
（2）第二次实验中两小球的质量之比mA:mB；
（3）第三次实验中三个小球上升的最大高度之比h1:h2:h3。

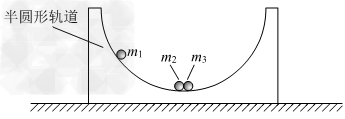
参考答案：解：（1）第一次实验中，小球的运动可以看做摆长为R的单摆，根据单摆周期公式有：

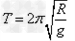
所以
（2）第二次实验中，球B从高为R处释放，设球B与球A碰撞前瞬间的速度大小为vB，碰撞后瞬间它们速度的大小分别为vB"和vA。由题意知，球B与A碰后达到的高度均为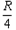，根据机械能守恒定律有



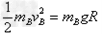
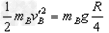
所以；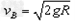
又根据动量守恒定律有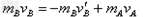
所以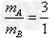
（3）根据题意设球1、2、3的质量分别为5m、3m和2m。设球1与球2碰撞前后的速度分别为v1、v1"，球2与球3碰撞前后的速度分别为v2、v2"，球3与球2碰撞后的速度为v3。球1与球2碰撞过程中动量守恒，且机械能守恒，则有
?
解得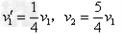
球2与球3碰撞过程中动量守恒，且机械能守恒，则有

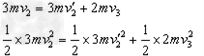
解得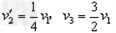
在三个小球的上升过程中，根据机械能守恒定律有
?
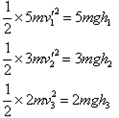解得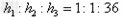

本题解析：

本题难度：困难

4、选择题  质量为m、速度为v的A球与质量为3m的静止B球发生正碰。碰撞可能是弹性的，也可能是非弹性的，因此，碰撞后B球的速度可能有不同的值。碰撞后B球的速度大小可能是
[? ]
A.0.6v
B.0.4v
C.0.2v
D.v

参考答案：B

本题解析：

本题难度：一般

5、计算题  如图所示，小球A系在细线的一端，线的另一端固定在O点，O点到水平面的距离为h。物块B质量是小球的5倍，置于粗糙的水平面上且位于O点正下方，物块与水平面间的动摩擦因数为μ。现拉动小球使线水平伸直，小球由静止开始释放，运动到最低点时与物块发生正碰（碰撞时间极短），反弹后上升至最高点时到水平面的距离为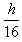。小球与物块均视为质点，不计空气阻力，重力加速度为g，求物块在水平面上滑行的时间t。

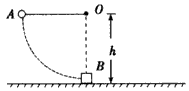
参考答案：解：设小球的质量为m，运动到最低点与物块碰撞前的速度大小为v1，取小球运动到最低点重力势能为零，根据机械能守恒定律，有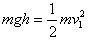
得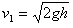
设碰撞后小球反弹的速度大小为v1"，同理有
得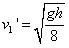
设碰后物块的速度大小为v2，取水平向右为正方向，根据动量守恒定律，有mv1=-mv1"+5mv2
得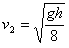
物块在水平面上滑行所受摩擦力的大小F=5μmg
设物块在水平面上滑行的时间为t，根据动量定理，有-Ft=0-5mv2
得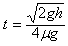

本题解析：

本题难度：困难