1、选择题  如图11所示器材可用来研究电感应现象及判定感应电流的方向。

参考答案：（1）略（2）BCD

本题解析：略

本题难度：简单

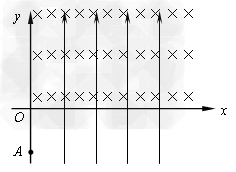
2、计算题  在xoy竖直平面内，仅在第一、四象限分布着竖直向上的匀强电场E，第一象限还存在着垂直纸面向里的匀强磁场B，方向如图所示。在y轴负向A点处有一质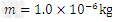量为，电量为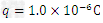的带正电微粒以初速度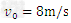，垂直y轴射入第四象限内。其中电场强度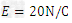，OA的长为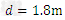，g取。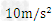
（1）微粒将打在x轴的P点，求OP的长l；
（2）如果带电微粒在P点进入第一象限，刚好与一质量也为m、不带电的微粒碰撞粘合在一起，形成一个新带电微粒，新微粒的质量为2m，电量为q，速度大小变为原来的一半，方向不变，则要使新微粒能再次打到x轴的正半轴上，则磁感应强度B应满足什么条件？

参考答案：解：（1）微粒在第四象限作类平抛运动

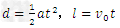
又由牛顿第二定律有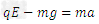
联立方程解之得l=4.8m
（2）微粒打在P点的速度为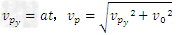
新微粒速度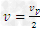，方向与水平方向成θ角

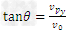
解之得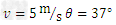
新微粒能再次打到x轴正方向上，其临界轨迹如图，设其半径为R，由几何关系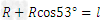

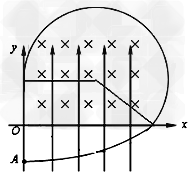
又由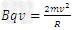

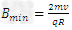
代入数据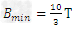

本题解析：

本题难度：一般

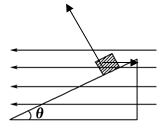
3、计算题  如图所示，一带电量为q＝－5×10－3 C，质量为m＝0.1 kg的小物块处于一倾角为θ＝37°的光滑绝缘斜面上，当整个装置处于一水平向左的匀强电场中时，小物块恰处于静止状态．(g取10 m/s2)：

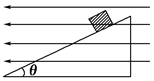
(1) 求电场强度多大？
(2)若从某时刻开始，电场强度减小为原来的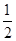，求物块下滑距离L＝1.5 m时的速度大小

参考答案：(1) 150N/C(2) 1.35J

本题解析：受力分析：竖直向下的重力，水平向右的电场力，垂直斜面向上的支持力

（1）N*cos37°=mg?①
Eq=N*sin37°?②
联立得? E=(mg*tan37°)/q=150N/C
（2）运用正交分解法
mg*sin37°-0.5*Eq*cos37°=ma
解得? a=0.3g
由动能定理：
mg*L*sin37°+0.5*Eq*L*cos37°=Ek-0
解得? Ek=0.9*mgL=1.35J
点评：本题难度较小，注意重力和电场力做功与路径无关，与初末位置有关

本题难度：简单

4、计算题  如图，在x＞0的空间中，存在沿x轴方向的匀强电场，电场强度E＝10 N/C；在x＜0的空间中存在垂直于xOy平面方向的匀强磁场，磁感应强度B＝0.5 T。一带负电的粒子（比荷q/m＝160 C/kg），在x＝0.06 m处的D点以v0＝8 m/s的初速度沿y轴正方向开始运动，不计带电粒子的重力。求：

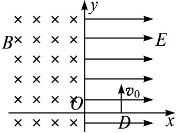
（1）带电粒子开始运动后第一次通过y轴时距O点的距离。
（2）带电粒子开始运动后第一次通过y轴的速度大小和方向；
（3）带电粒子进入磁场后经多长时间返回电场；

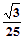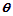参考答案：（1）沿y轴方向的位移y=v0t1=m （2）v==16m/s，即=60°
（3）运动时间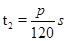

本题解析：（1）粒子在第一象限做类平抛运动，如图所示，

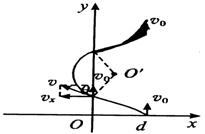
加速度a=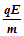=1600m/s2，运动时间t1=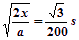，沿y轴方向的位移y=v0t1=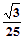m
（2）粒子通过y轴进入磁场时在x方向上的速度vx=at1=8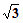m/s，v==16m/s，
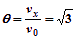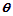因此tan，即=60°
（3）粒子在第二象限以O1为圆心做匀速圆周运动，圆弧所对的圆心角为2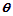=120°，运动时间t2=T=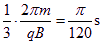
点评：本题主要考查了带电粒子在混合场中运动的问题，要求同学们能正确分析粒子的受力情况，再通过受力情况分析粒子的运动情况，熟练掌握圆周运动及平抛运动的基本公式，难度适中．

本题难度：一般

5、选择题  如图所示，匀强磁场和匀强电场相互垂直，一电子以某一速度飞入其中后，做匀速直线运动，其速度方向应该为（?）

A．垂直纸面向里
B．与电场线平行
C．与磁感线平行
D．垂直纸面向外

参考答案：D

本题解析：电子以某一速度飞入其中后，做匀速直线运动，电子所受的电场力和洛伦兹力的合力为零。
A．若电子运动方向垂直纸面向里，电场力竖直向上，开始运动时洛伦兹力竖直向上，不符合题意，A错误。
B．若电子运动方向与电场线平行，电场力竖直向上，开始运动时洛伦兹力向里或向外，不符合题意，B错误。
C．若电子运动方向与磁感线平行电场力竖直向上，开始运动时洛伦兹力为零，不符合题意，C错误。
D．若电子运动方向，垂直纸面向外电子所受的电场力和洛伦兹力的合力为零，符合题意，故选D。
点评：理解电子做匀速直线运动的条件，准确的掌握右手定则判断负电荷所受洛伦兹力的方向，是解决本题的关键。

本题难度：一般