1、计算题  如图a所示，一个质量为m = 2.O×1O-11kg，电荷量q =1.O×1O-5C的带负电粒子(重力忽略不计)，从静止开始经U1=100V电压加速后，垂直于场强方向进入两平行金属板间的匀强偏转电场。偏转电场的电压U2=100V，金属板长L=20cm，两板间距d =1Ocm．

小题1:粒子进人偏转电场时的速度v0大小；
小题2:粒子射出偏转电场时的偏转角θ；
小题3:在匀强电场的右边有一个足够大的匀强磁场区域。若以粒子进入磁场的时刻为t =0，磁感应强度B的大小和方向随时间的变化如图b所示，图中以磁场垂直于纸面向内为正。如图建立直角坐标系(坐标原点为微粒进入偏转电场时初速度方向与磁场的交边界点)。求在t =×10-6s时粒子的位置坐标(X，Y)。(答案可以用根式表示，如用小数，请保留两位有效数字)

参考答案：
小题1:1.0×104m/s
小题2: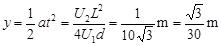
小题3:

本题解析：（1）粒子在加速电场中由动能定理得
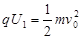?解得v0=1.0×104m/s?（3分）
（2）粒子在偏转电场中做类平抛运动，有?
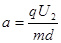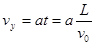（1分），?（1分）
飞出电场时，速度偏转角的正切：
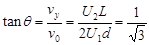?（2分）
解得?θ="30°?" （1分）
飞出电场时，偏转距离
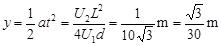?（1分）
（3）进入磁场时粒子的速度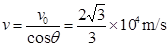?（1分）

设粒子在磁场中做圆周运动的周期为T，圆周运动半径为r。则由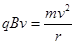
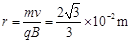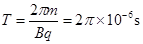得?（1分）
?（1分）
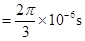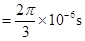依题意，知粒子在t=0到t内和在t到t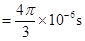时间内在磁场中转过的圆弧所对的圆心角均为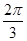，粒子的运动轨迹应如图所示。
由几何关系得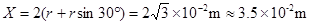?（2分）

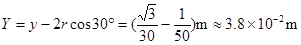
本题难度：一般

2、计算题  （18分）如图，在第二象限的圆形区域I存在匀强磁场，区域半径为R，磁感应强度为B，且垂直于Oxy平面向里;在第一象限的区域II和区域III内分别存在匀强磁场，磁场宽度相等，磁感应强度大小分别为B和2B，方向相反，且都垂直于Oxy平面。质量为m、带电荷量q（q＞0）的粒子a于某时刻从圆形区域I最高点Q（Q和圆心A连线与y轴平行）进入区域I，其速度v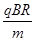＝?。已知a在离开圆形区域I后，从某点P进入区域II。该粒子a离开区域II时，速度方向与x轴正方向的夹角为30°；此时，另一质量和电荷量均与a相同的粒子b从P点进入区域II，其速度沿x轴正向，大小是粒子a的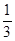。不计重力和两粒子之间的相互作用力。求：
（1）区域II的宽度；
（2）当a离开区域III时，a、b两粒子的y坐标之差.

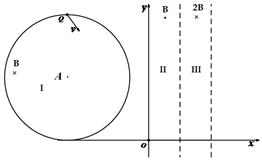
参考答案：（1）?（2）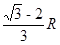

本题解析：（1）如图所示，a粒子进入区域I后，由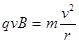
故a粒子在区域I做圆周运动的半径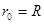?…………（1分）
其轨迹圆心为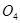,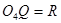且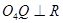
由几何知识得：
a粒子从某点D出射时，速度v沿x轴正方向. …………（2分）
a粒子从P点沿x轴正方向进入区域II后，由
得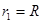?，可找到圆心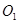?…………（1分）
作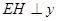轴，由图知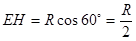：?，即磁场区域宽度?…………（2分）
(2)①对a粒子的运动进行分析：
进入区域Ⅲ后，由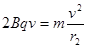，得……..（1分）
连接O1E并延长，取EO2=r2，则O2为a粒子在区域Ⅲ中的轨迹圆心延长HE交Ⅲ右边界于F，连接O2F
由已知条件易证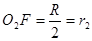，故F点是a粒子在区域Ⅲ中的出射点
且轨迹所对应的圆心角为60o
故a粒子在区域Ⅲ中运动的时间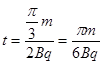…..（1分）
由图根据几何关系知：…..（1分）
②对b粒子的运动进行分析：
b粒子进入区域Ⅱ后，由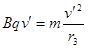，得：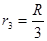
且其轨迹圆心O3位于y轴上
P点进入区域II，运动时间为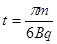?，故其轨迹所对应的圆心角为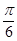…（1分）
由图根据几何知识：?…………（1分）
综上分析可知：
当a离开区域III时，a、b两粒子的y坐标之差为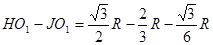
即坐标差为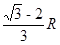? …………（2分）

本题难度：一般

3、计算题  （18分）如图所示装置的左半部分为速度选择器，相距为d的两块平行金属板分别连在电压可调的电源两极上（上板接正极），板间存在方向垂直纸面向里、磁感应强度为B0的匀强磁场；右半部分为一半径为R的半圆形磁场区域，内有垂直纸面向外、磁感应强度为B的匀强磁场．矩形abcd相切于半圆，小孔M、N连线延长线经过圆心O点且与ad垂直．一束质量为m、带电量为+q的离子（不计重力）以不同速率沿MN方向从M孔射入．

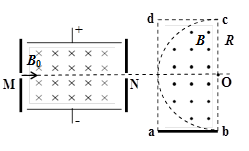
（1）金属板间电压为U0时，求从N孔射出的离子的速度大小；
（2）要使离子能打到ab上，求金属板间电压U的取值范围．

参考答案：（1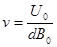）   （2）

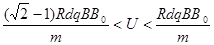
本题解析：（1）设电压为U0时，两板间电场强度为E，从N孔射出的粒子速度为v，则
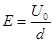 ①，  由平衡条件得 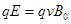②
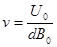解得：  ③
（2）如答图(

本题难度：一般

4、计算题  如图所示，通电导体棒AC静止于水平导轨上，棒的质量为m长为L，通过的电流强度为I，匀强磁场的磁感强度B的方向与导轨平面成θ角，求导轨受到AC棒的压力和摩擦力各为多大？

参考答案：mg-BIlcosθ，BIlsinθ

本题解析：导体棒AC静止于水平导轨上，受到重力、安培力、导轨的支持力和静摩擦力．导体棒与磁场方向垂直，安培力大小FA=BIl，根据左手定则判断安培力方向，根据平衡条件求解导轨对导体棒的支持力和摩擦力，再由牛顿第三定律求解导轨受到AC棒的压力和摩擦力．

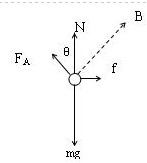
以导体棒AC为研究对象，分析受力，如图．
其中，安培力大小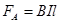，根据平衡条件得
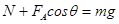?①
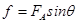?②
由①得，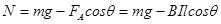
由②得，?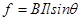
由牛顿第三定律得，导轨受到AC棒的压力和摩擦力各为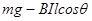和．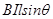
点评：做此类型的问题时安培力是桥梁，关键是安培力的方向判断和大小计算．

本题难度：一般

5、计算题  汤姆生曾采用电场、磁场偏转法测定电子的比荷，具体方法如下：
Ⅰ．使电子以初速度v1垂直通过宽为L的匀强电场区域，测出偏向角θ，已知匀强电场的场强大小为E，方向如图（a）所示

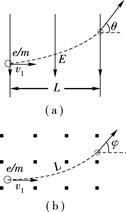
Ⅱ．使电子以同样的速度v1垂直射入磁感应强度大小为B、方向如图（b）所示的匀强磁场，使它刚好经过路程长度为L的圆弧之后射出磁场，测出偏向角φ，请继续完成以下三个问题：
（1）电子通过匀强电场和匀强磁场的时间分别为多少？
（2）若结果不用v1表达，那么电子在匀强磁场中做圆弧运动对应的圆半径R为多少？
（3）若结果不用v1表达，那么电子的比荷e / m为多少？

参考答案：（1）t=L/v1；（2）R=L/φ；（3）e/m=

本题解析：（1）电子通过匀强电场和匀强磁场的时间相等，分别都是：t=L/v1…………①（2分）
（2）电子进入匀强磁场中作匀速圆周运动有：R=L/φ…………………… ②（2分）
（3）沿电场力方向有：vy=at=eEL/mv1………………………………………③（1分）
电子射出电场时的速度偏向角满足：tanθ=vy/v1…………………………④（1分）
由牛顿第二定律，有：e v1B =" m" ………………………………………⑤（1分）
综合②③④⑤，解得：e/m=………………………………………………⑥（2分

本题难度：一般