1、简答题 如图所示,有一根长2L的轻质细线,它的两端固定在一根长为L的竖直转轴AB上,线上套一个可以自由移动的质量为m的小环.当转轴转动时小环正好以B为圆心,在水平面内作匀速圆周运动.求
(1)线的张力.
(2)小环的线速度.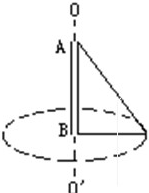
参考答案:
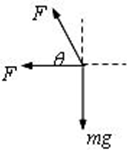
设小球做匀速圆周运动的半径为r,则线长和半径之间的关系为
? (2L-r)2=r2+L2,解得r=34L.?
则斜线与水平方向的夹角θ=53°
对小球受力分析如图所示,由牛顿第二定律可得
? F+Fcosθ=mv2r?
? Fsinθ=mg?
联立两式,解得F=54mg,v=
本题解析:
本题难度:一般
2、选择题 关于直线运动的下述说法正确的是( )
A.加速度不变的作直线运动物体的速度是恒定的,不随时间改变
B.加速度不变的作直线运动物体的瞬时速度随时间而改变
C.若物体的速度随时间不断增加,则物体的位移将一直在减少
D.若物体的速度随时间不断减小,则物体位移也将一直在减少
参考答案:A、加速度不变的直线运动是匀变速直线运动,速度随时间均匀增大.故A错误,B正确.
? C、速度随时间不断增加,速度方向不变,则位移增加.故C错误.
?D、速度随时间减小,只要速度方向不变,则位移增加.故D错误.
故选B.
本题解析:
本题难度:一般
3、选择题 如图所示,长为L的轻杆A一端固定一个质量为m的小球B,另一端固定在水平转轴O上,轻杆A绕转轴O在竖直平面内匀速转动,角速度为ω。在轻杆A与水平方向夹角α从0°增加到90°的过程中,下列说法正确的是?
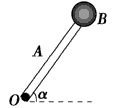
[? ]
A.小球B受到轻杆A作用力的方向一定沿着轻杆A
B.小球B受到的合力的方向一定沿着轻杆A
C.小球B受到轻杆A的作用力逐渐减小
D.小球B受到轻杆A的作用力对小球B做正功
参考答案:BCD
本题解析:
本题难度:一般
4、简答题 如图所示,在坐标系xOy内有一半径为a的圆形区域,圆心坐标为O1(a,0),圆内分布有垂直纸面向里的匀强磁场.在直线y=a的上方和直线x=2a的左侧区域内,有一沿y轴负方向的匀强电场,场强大小为E.一质量为m、电荷量为+q(q>0)的粒子以速度v从O点垂直于磁场方向射入,当速度方向沿x轴正方向时,粒子恰好从O1点正上方的A点射出磁场,不计粒子重力.
(1)求磁感应强度B的大小;
(2)若粒子以速度v从O点垂直于磁场方向射入第一象限,当速度方向沿x轴正方向的夹角θ=30°时,求粒子从射入磁场到最终离开磁场的时间t.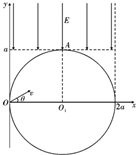
参考答案:(1)设粒子在磁场中做圆运动的轨迹半径为R?qvB=mv2R
粒子自A点射出,由几何知识?R=a
解得?B=mvqa
(2)粒子在磁场中做圆运动的周期?T=2πav
粒子从磁场中的P点射出,因磁场圆和粒子的轨迹圆的半径相等,OO1PO2构成菱形,故粒子从P点的出射方向与y轴平行,粒子由O到P所对应的圆心角为?θ1=600
由几何知识可知,粒子由P点到x轴的距离?S=acosθ
粒子在电场中做匀变速运动,根据动量定理得:qEt1=2mv;
在电场中运动的时间?t1=2mvqE
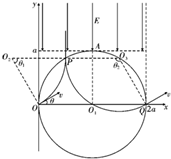
粒子由P点第2次进入磁场,由Q点射出,PO1QO3构成菱形,由几何知识可知Q点在x轴上,粒子由P到Q的偏向角为θ2=1200,则?θ1+θ2=π
粒子先后在磁场中运动的总时间?t2=T2⑦
粒子在场区之间做匀速运动的时间?t3=2(a-S)v⑧
解得粒子从射入磁场到最终离开磁场的时间?t=t1+t2+t3=(2+π-
本题解析:
本题难度:一般
5、选择题 下列各组物理量中都是矢量的是( )
A.弹力速度路程
B.长度质量时间
C.长度速度变化量加速度
D.位移重力加速度