1、简答题  在竖直平面内建立一平面直角坐标系xoy，x轴沿水平方向，如图甲所示．第二象限内有一水平向右的匀强电场，场强为E1．坐标系的第一、四象限内有一正交的匀强电场和匀强交变磁场，电场方向竖直向上，场强E2=

参考答案：

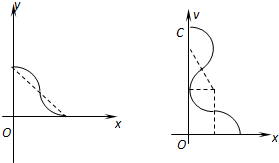
（1）将粒子在第二象限内的运动分解为水平方向和竖直方向，在竖直方向上做竖直上抛运动，在水平方向上做匀加速直线运动．
t=v0g=0.4s．
h=v02t=0.8m．
ax=v1t=2g，
则qE1=2mg，解得E1=0.2N/C．
（2）qE2=mg，所以带电的粒子在第一象限将做匀速圆周运动，设粒子运动圆轨道半径为R，周期为T，则qv1B0=mv12R可得R=0.08B0．
使粒子从C点运动到D点，则有：h=(2n)R=(2n)0.08B0．
解得：B0=0.2n（T）（n=1，2，3…）．
T=2πmqB0．
T02=T4，
T0=T2=πmqB0=π20n(s)?(n=1，2，3…)．
（3）当交变磁场周期取最大值而粒子不再越过y轴时可作如图运动情形：
由图可知θ=5π6
T0≤56T=5π300B0．
B0T0≤π60(kg/C)．
答：（1）带电微粒运动到C点的纵坐标值h为0.8m．电场强度E1为0.2N/C．
（2）磁感应强度B0为B0=0.2n（T）（n=1，2，3…）．磁场的变化周期T0为T0=T2=πmqB0=π20n(s)?(n=1，2，3…)．
（3）交变磁场磁感应强度B0和变化周期T0的乘积B0 T0应满足B0T0≤π60(kg/C)．

本题解析：

本题难度：一般

2、简答题  如图，光滑水平面AB与竖直面内的光滑半圆形固定轨道在B点相切，半圆形轨道半径为R=2.5m，一个质量m=0.5kg的小物块压缩弹簧，静上在A处，释放小物块，小物块离开弹簧后经B点进入轨道，经过C点时对轨道的压力为其重力的3倍．取g=10m/s2．求：
（1）小物块经过C点时速度的大小？
（2）弹簧对小物块的弹力做的功？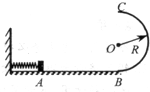

参考答案：（1）小球在C点，由牛顿第二定律得：
F+mg=mv2CR，F=3mg，
解得：vC=2

本题解析：

本题难度：一般

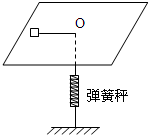
3、简答题  做圆轨道上稳定运行的飞船内，宇航员为了验证向心力公式，设计了如图所示的装置（图中O为光滑的小孔）：给待测物体一个初速度，使它在水平桌面上做匀速圆周运动．该飞船内具有基本测量工具．
（1）实验时需要测量的物理量是______；（写出描述物理量的文字和符号）
（2）若向心力公式成立，则上述物理量的关系式：______．

参考答案：据题，物体在桌面上做匀速圆周运动，物体与桌面间的摩擦力忽略不计，由弹簧秤的拉力提供物体的向心力．根据牛顿第二定律得：
F=m(2nπt)2r
所以实验时需要测量的物理量是弹簧秤示数F、物块质量m、物块到小孔O的距离r、物块转n圈时间t．
故答案为：弹簧秤示数F、物块质量m、物块到小孔O的距离r、物块转n圈时间t；F=m(2nπt)2r

本题解析：

本题难度：一般

4、选择题  如图所示，质量为m的小球在竖直面内的光滑圆轨道内侧做半径为R的圆周运动，不计空气阻力，设小球恰好能通过最高点B时速度的大小为v．若小球在最低点以大小为2v的速度水平向右运动，则下列说法正确的是（　　）
A．小球在最低点对轨道的压力大小为5mg
B．小球能通过轨道的最高点B
C．小球不能通过轨道上与圆心等高的A点
D．小球在AB之间某一点脱离圆轨道，此后做平抛运动