1、选择题  用一根横截面积为S、电阻率为ρ的硬质导线做成一个半径为r的圆环，AB为圆环的一条直径。如图所示，在AB的左侧存在一个均匀变化的匀强磁场，磁场垂直圆环所在平面，方向如图所示，磁感应强度大小随时间的变化率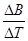?＝k（k<0）。则（　　）

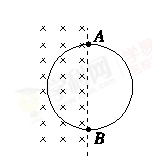
A．圆环中产生逆时针方向的感应电流
B．圆环具有扩张的趋势
C．圆环中感应电流的大小为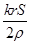
D．圆环具有收缩的趋势

参考答案：B

本题解析：
试题分析: 磁场方向垂直纸面向里，磁感应强度大小随时间的变化率ΔB/Δt＝k（k<0），说明B减少，穿过圆环的磁通量减少，由楞次定律判断可知：圆环中产生的感应电流方向沿顺时针方向，故A错误．穿过圆环的磁通量减少，由楞次定律可知，圆环为了阻碍磁通量的减少，圆环应有扩展的趋势，故B正确，D错误；
C、由法拉第电磁感应定律得E=Δφ/Δt=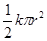，圆环的电阻R=ρ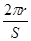，则感应电流大小为 I=，故C错误．

本题难度：简单

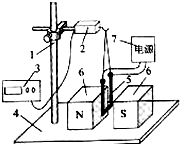
2、选择题  利用如图所示的实验装置可以测量磁感应强度．其中2为力敏传感器，3为数字电压表，5为底部长为L的线框．当外界拉力作用于力敏传感器的弹性梁上时，数字电压表上的读数U与所加外力F成正比，即U=KF，式中K为比例系数．用绝缘悬丝把线框固定在力敏传感器的挂钩上，并用软细铜丝连接线框与电源．当线框中电流为零时，输出电压为U0；当线框中电流为I时，输出电压为U．则磁感应强度的大小为（　　）
A．B=

参考答案：A、由于数字电压表上的读数U与所加外力成正比，即U=KF，式中K为比例系数，当通上电流后，设安培力为FA，有

本题解析：

本题难度：简单

3、简答题  如图一所示，竖直面上有两电阻不计的光滑金属导轨平行固定放置，间距d为0，5m，上端通过导线与阻值为2Ω的电阻R连接，下端通过导线与阻值为4Ω的小灯泡L连接，在CDEF矩形区域内有水平向外的匀强磁场，磁感应强度B随时间变化如图二所示，CE长为2m．在t=0时，电阻2Ω的金属棒以某一初速度从AB位置紧贴导轨向下运动，当金属棒从AB位置运动到EF位置过程中，小灯泡的亮度没有发生变化，g取10m/s2．求：
（1）通过小灯泡的电流强度
（2）金属棒的质量
（3）t=0.25s时金属棒两端的电势差
（4）金属棒从AB位置运动到EF位置过程中，电阻R中的焦耳热．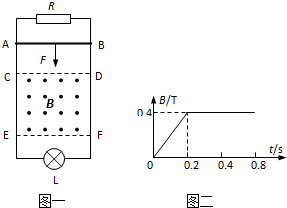

参考答案：（1）金属棒未进入磁场时，E1=△?△t=S△B△t=0.5×2×0.40.2=2?V?
R总=RL+R2=4+1=5Ω?
IL=E1R总=25=0.4A?
（2）因灯泡亮度不变，故0.2s末金属棒进入磁场时刚好匀速运动，
I=IL+IR=IL+ILRLR=0.4+0.4×42=1.2?A?
G=FA=BId=0.4×1.2×0.5=0.24?N?
所以金属棒的质量：m=Gg=0.024Kg?
（3）金属棒在磁场中运动时电动势E2=I（R+RRLR+RL）=1.2（2+2×42+4）=4V?
v=E2Bd=40.4×0.5=20m/s
金属棒从CD位置运动到EF位置过程的时间为t2=CEv=220s=0.1s，在这段时间内U=ILRL=0.4×4V=1.6V，所以t=0.25s时金属棒两端的电势差为1.6V?
（4）金属棒在进入磁场前，电阻R中的焦耳热Q1=I12Rt=0.22×2×0.2J=0.016J
金属棒从AB位置运动到EF位置过程中的焦耳热Q2=I22Rt=0.82×2×0.1J=0.128J
金属棒从AB位置运动到EF位置过程中，电阻R中的焦耳热Q=Q1+Q2=0.144J
答：（1）通过小灯泡的电流强度是0.4A；
（2）金属棒的质量是0.024kg；
（3）t=0.25s时金属棒两端的电势差为1.6V；
（4）金属棒从AB位置运动到EF位置过程中，电阻R中的焦耳热为0.144J．

本题解析：

本题难度：一般

4、填空题  如图，理想变压器原、副线圈的匝数之比n1：n2=4：1，原线圈两端连接光滑导轨，副线圈与电阻R相连接组成闭合回路．当直导线AB在垂直于导轨平面的匀强磁场中沿导轨匀速向右作切割磁感线运动时，安培表A1的读数为12mA，那么安培表A2的读数为______A．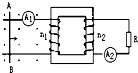

参考答案：由于直导线AB匀速运动，则AB切割磁场产生的电流时恒定的，线圈产生的磁通量也是恒定的，所以不会引起副线圈的磁通量的变化，所以副线圈不会有感应电流产生，即安培表A2的读数为0．
故答案为：0．

本题解析：

本题难度：简单

5、简答题  如图所示，AB、CD是两根足够长的固定平行金属导轨，两导轨间的距离为L，导轨平面与水平面的夹角为θ，在整个导轨平面内都有竖直向上的匀强磁场，磁感应强度为B，在导轨的?AC端连接一个阻值为?R的电阻，一根质量为m、垂直于导轨放置的金属棒ab，从静止开始沿导轨下滑，求此过程中ab棒的最大速度．已知ab与导轨间的动摩擦因数为μ，导轨和金属棒的电阻都不计．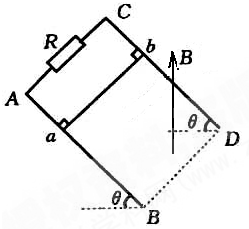

参考答案：金属棒ab先做加速度减小的变加速运动，后做匀速直线运动，此时速度达到最大，设最大速度为vm．此时金属棒产生的感应电动势为：


E=BLvmcosθ
金属棒所受的安培力大小为：F=BIL，金属棒受力如图．
又 I=ER，得 F=B2L2vmcosθR
根据平衡条件得：
? mgsinθ=Fcosθ+f
又f=μ（mgcosθ+Fsinθ）
联立解得：vm=mg(sinθ-μcosθ)RB2L2(cosθ+μsinθ)cosθ．
答：此过程中ab棒的最大速度为mg(sinθ-μcosθ)RB2L2(cosθ+μsinθ)cosθ．

本题解析：

本题难度：一般