D.1.4π
参考答案:设登月器和航天飞机在半径3R的轨道上运行时的周期为T,
因其绕月球作圆周运动,
所以应用牛顿第二定律有
GMmr2=m4π2rT2 r=3R
T=2π
本题解析:
本题难度:简单
2、选择题 要使两物体间万有引力减小到原来的1/4,可采取的方法是
[? ]
A.使两物体的质量各减少一半,距离保持不变
B.使两物体间距离变为原来的2倍,质量不变
C.使其中一个物体质量减为原来的1/4,距离不变
D.使两物体质量及它们之间的距离都减为原来的1/4
参考答案:ABC
本题解析:
本题难度:简单
3、选择题 2012年9月采用一箭双星的方式发射了“北斗导航卫星系统”(BDS)系统中的两颗圆轨道半径均为21332km的“北斗-M5”和“北斗M-6”卫星,其轨道如图所示。关于这两颗卫星,下列说法正确的是( ?)
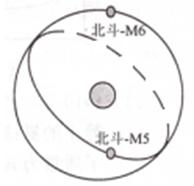
A.两颗卫星绕地球运行的向心加速度大小相等
B.两颗卫星绕地球的运行速率均大于7.9km/s
C.北斗-M5绕地球的运行周期大于地球的自转周期
D.北斗-M6绕地球的运行速率大于北斗-M5的运行速率
参考答案:A
本题解析:
试题分析: 根据 =ma知,轨道半径相等,则向心加速度大小相等.故A正确;根据v= =ma知,轨道半径相等,则向心加速度大小相等.故A正确;根据v=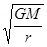 知,轨道半径越大,线速度越小,第一宇宙速度的轨道半径等于地球的半径,是做匀速圆周运动的最大速度,所以两颗卫星的速度均小于7.9km/s.故B错误;根据T= 知,轨道半径越大,线速度越小,第一宇宙速度的轨道半径等于地球的半径,是做匀速圆周运动的最大速度,所以两颗卫星的速度均小于7.9km/s.故B错误;根据T= ,北斗-M6的轨道半径小于同步卫星的轨道半径,则北斗-M5绕地球的运行周期小于地球的自转周期.故C错误;根据v= ,北斗-M6的轨道半径小于同步卫星的轨道半径,则北斗-M5绕地球的运行周期小于地球的自转周期.故C错误;根据v=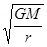 知北斗-M6绕地球的运行速率等于北斗-M5的运行速率,故D错误。 知北斗-M6绕地球的运行速率等于北斗-M5的运行速率,故D错误。
本题难度:一般
4、简答题 已知地球的半径R≈6.4×106m,地球表面的重力加速度g≈10m/s2,万有引力恒量G≈6.7×10-11N·kg2/m2。由此推导并估算:(把结果只保留一位有效数字即可)
(1)地球的质量M约为多少?
(2)近地环绕卫星的最大线速度v1约为多少?
参考答案:(1)R2g/G?(2)8×103m/s
本题解析:(1)由重力的概念知:G =mg……………….………..①(3分) =mg……………….………..①(3分)
∴M=R2g/G…………………………………………………………………..…………②(2分)
即M=(6.4×106)2×106/7×10-11≈6×1024kg……………………….…….(3分)
(2)对质量为m的近地卫星,应用牛Ⅱ律有:
mg=mv2/R………………………………………………………………….…………..③(3分)
∴v=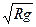 ……………………………………………………………….….………….(2分) ……………………………………………………………….….………….(2分)
≈8×103m/s……………………………………………………..…………(3分)
本题难度:简单
5、计算题 宇宙中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行。设每个星体的质量均为m。
(1)试求第一种形式下,星体运动的线速度和周期。
(2)假设两种形式星体的运动周期相同,第二种形式下星体之间的距离应为多少?
参考答案:解:(1)第一种形式下,由万有引力和牛顿第二定律得
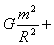 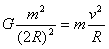
解得 ,周期 ,周期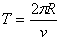
得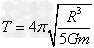
(2)第二种形式下,由万有引力和牛顿第二定律得
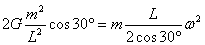
角速度: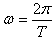
解得
本题解析:
本题难度:困难
|