1、选择题  一小球沿斜面匀加速滑下，依次经过A、B、C三点。已知AB=3m，BC=5m，小球经过AB和BC两段所用的时间均为2s，则小球的加速度大小和经过A点时的速度大小分别是(    )
A．0.5 m/s2   1 m/s    B．1 m/s2   2 m/s   C．0.5 m/s2   2 m/s    D．1 m/s2   1m/s

参考答案：A

本题解析：根据匀变速直线运动过程中在相等时间内走过的位移差是一个定值可得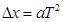：，故，根据匀变速直线运动过程中中间时刻速度等于全程平均速度可得中间时刻的速度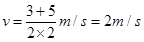，故A点的速度为：，故A正确；
考点：考查了匀变速直线运动规律的应用

本题难度：一般

2、计算题  一列货车以8m/s的速度在铁路上行驶，由于调度事故，在货车后面600m处有一列快车以20m/s的速度在同一轨道上行驶，快车司机赶快合上制动器，但快车要滑行2000m才停下来，请判断两车会不会相撞？

参考答案：解：快车刹车后的加速度大小为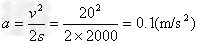
当两车速度相等时，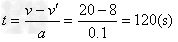
快车多走距离为：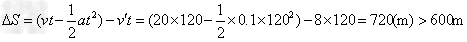
或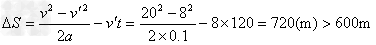
故两车将相撞

本题解析：

本题难度：一般

3、选择题  某物体做匀变速直线运动，经过A点时的速度V0=4m/s，加速度为a=-2m/s2，则当它运动到距离A点3米处时需要时间可能为（　　）
A．1s
B．3s
C．

参考答案：设物体向右做匀变速直线运动，经过A点时的速度V0=4m/s，加速度为a=-2m/s2，
则当它运动到A点右侧，距离A点3米处，根据匀变速直线运动的位移时间公式x=v0t+12at2得：
3=4t+12×(-2)t2
解得：t1=1s，t2=3s．
当它运动到A点左侧，距离A点3米处，有：
-3=4t+12×(-2)t2
解得：t1′=2+

本题解析：

本题难度：一般

4、选择题  物体静止在光滑水平面上，对物体施一水平向右的恒力F1，经过时间t突然撤去F1，立即对它施一水平向左的恒力F2，又经过时间t物体恰好到达出发点．则两段时间内（　　）
A．加速度a1和a2大小之比为1：2
B．最大速度υ1m和υ2m大小之比为2：1
C．通过的位移x1和x2大小之比是1：3
D．F1、F2对该物体做功的最大即时功率之比是1：6

参考答案：A、物体从静止起受水平恒力F1 作用，做匀加速运动，经一段时间t后的速度为V1=a1t=F1mt
以后受恒力F2，做匀减速运动 a2=F2m
经同样时间后回到原处，整个时间内再联系物体的位移为零，
于是12a1t2+v1t-12a2t2=0
解得 F2=3F1，
所以加速度之比1：3，故A错误；
B、v2=v1-a2t=(F1-F2)mt
所以v2：v1=(F1-F2)F1=-2
即v2：v1速度大小比为：2：1
最大速度υ1m和υ2m大小之比为1：2，故B错误；
C、通过的位移大小相等，所以位移之比为1；1，故C错误；
D、最大功率P=Fvm
所以F1、F2对该物体做功的最大即时功率之比是F1v1：F2v2=1：6，故D正确．
故选D

本题解析：

本题难度：一般

5、简答题  一水平传送带以2.0m/s的速度顺时针传送，水平部分长为2.0m，其右端与一倾角为θ=37°的光滑斜面平滑相连，斜面长为0.4m，一个可视为质点物块无初速度地放在传送带最左端，已知物块与传送带间动摩擦因数μ=0.2，试问：
（1）物块能否达斜面顶端？若能则说明理由，若不能则求出物块上升的最大高度．
（2）出发后9.5s内物块运动的路程．（sin37°=0.6，g取10m/s2）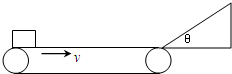

参考答案：（1）物块在传送带上先加速后匀速，在摩擦力作用下产生加速度大小为：a1=μg=2(m/s2)
物体做匀加速运动的时间为：t1=v0a1=1（s）；
匀加速运动的距离为：S1=12a1t21=1(m)
剩下物体匀速距离为：S2=L-S1=1(m)；匀速时间为：t2=S2v0=0.5(s)
然后物块以2m/s的速度滑上斜面，
因为斜面光滑，所以物体在斜面上运动的加速度大小为：a2=gsinθ=6(m/s2)
上升过程历时：t3=v0a2=13(s)；上升距离S3=v202a2=13(m)＜0.4m．
所以没有到最高点，上升高度为h=S3sinθ=0.2（m）
（2）物块的运动全过程为：
先匀加速1s，匀速运动0.5s，在斜面上匀减速上升13s，在斜面上匀加速下降13s后回到传送带，再经过1s速度减为零，然后加速1s运动到斜面底端…如此往复，周期为83s．
由第一次到达斜面底端算起，还剩8s，恰好完成三个周期∴S=L+6（S1+S3）=10（m）
答：（1）不能到达斜面顶端，上升的最大高度为0.2m；
（2）出发后9.5s内物体的路程为10m．

本题解析：

本题难度：一般