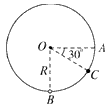
1、计算题  如图所示，半径为R的光滑绝缘圆环固定在竖直平面内，在环的底端B点固定一个带正电的小珠，环上还套有一个质量为m，带有与小珠等量正电荷的小球，现将小球从A点（半径OA水平）由静止释放开始运动，当运动到C点（∠AOC=30。）时获得的最大动能为Ekm，求
（1）小球在A点刚释放时运动的加速度？
（2）小球从位置A运动到位置C的过程中所受静电力做的功？
（3）小球在位置C时受到圆环对它的作用力？

参考答案：（1）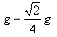
（2）Ekm-1/2mgR
（3）mg+2Ekm/R

本题解析：

本题难度：一般

2、选择题  如图所示，物体A放在物体B上，物体B放在光滑的水平面上，已知mA=6kg，mB=2kg，A、B间动摩擦因数μ＝0.2，A物上系一细线，细线能承受的最大拉力是20N，水平向右拉细线，假设最大静摩擦力等于滑动摩擦力。下述中正确的是(g＝10m/s2)?
?
A．当拉力F<12N时，A静止不动
B．当拉力F>12N时，A相对B滑动
C．当拉力F＝16N时，B受A摩擦力等于4N
D．只要绳子未被拉断，A相对B始终静止?

参考答案：CD

本题解析：设整体一直一起向右运动，则根据整体法可知，即最大加速度，此刻对于B物体而言受到向前的静摩擦力应该为，没有超过最大静摩擦力，所以D正确。当B受到摩擦力为4N时，整体加速度为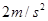，所以整体的受到的拉力应该为，C对。
点评：本题通过整体法与隔离法考察了牛顿第二定律的运用，在整个过程中AB之间的最大静摩擦力是一个临界点。

本题难度：一般

3、计算题  如图14所示，车厢内的小桌上固定一光滑斜面，除去小球车厢的总质量为M、小球的质量为m，斜面倾角为α。车在水平推力作用下向右做匀加速直线运动，小球（视为质点）始终与车相对静止，小球距桌面的高度为h，距车厢地板高度为H，离桌面边缘水平距离为L，离车厢前壁的距离为d。车在运动过程中所受的阻力等于车对地面压力的k倍，重力加速度为g。
（1）求水平推力F1的大小
（2）若M=10kg，m=1kg，α=37°， k=0.20，h=0.20m，H=0.80m，L=0.30m，d=1.60m，g=10m/s2。当车速为v0=15m/s时，撤去推力F1同时对车施加水平向左的拉力F2（如虚线所示），小球立即离开斜面向右飞去。为使小球在运动中不碰到桌子和前壁，所加拉力F2应满足什么条件？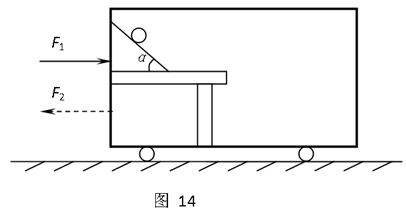

参考答案：（1）F1=（M+m）g（k+tanα）
（2）130N<F2<180N

本题解析：略

本题难度：简单

4、计算题  （8分）如图所示，在倾角为θ的光滑斜面上端系有一劲度系数为k的轻质弹簧，弹簧下端连一个质量为m的小球，球被一垂直于斜面的挡板A挡住，此时弹簧没有形变．若挡板A以加速度a（a＜gsinθ）沿斜面向下匀加速运动，问：
?
（1）小球向下运动多少距离时速度最大？
（2）从开始运动到小球与挡板分离所经历的时间为多少？

参考答案：（1）xm＝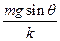
（2）t＝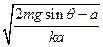

本题解析：（1）球和挡板分离后做加速度减小的加速运动，当加速度为零时，速度最大，此时物体所受合力为零．
即kxm＝mgsinθ，?（2分）
解得xm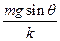＝.?（1分）
（2）设球与挡板分离时位移为s，经历的时间为t，从开始运动到分离的过程中，m受竖直向下的重力，垂直斜面向上的支持力FN，沿斜面向上的挡板支持力F1和弹簧弹力F.
据牛顿第二定律有mgsinθ－F－F1＝ma，?（1分）
F＝kx.?（1分）
随着x的增大，F增大，F1减小，保持a不变，当m与挡板分离时，x增大到等于s，F1减小到零，则有：?mgsinθ－ks＝ma，?（1分）
又：?s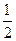＝at2?（1分）
联立解得：mgsinθ－k·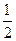at2＝ma，
t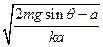＝.?（1分）

本题难度：简单

5、简答题  
（1）滑板受到的阻力大小；
（2）运动员匀加速下滑至底端时所需的时间。

参考答案：（1）50N（2）s

本题解析：（1）匀减速上滑，受力分析如图，选取沿斜面向上为正方向


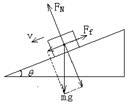
由?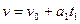
得a1=-6m/s2?----------(1分)
由牛顿第二定律可得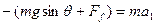：?-------(2分)
解得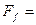：50N? ----------(1分)
（2）匀加速下滑，受力分析如图，选取沿斜面向下为正方向
由牛顿第二定律可得：?
代入数据可得：a2=4m/s2?-------(2分)
运动员上滑的位移为：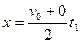
可得：x=12m?-------(2分)
下滑的位移与上滑时的位移相同，设下滑的时间为t2
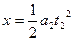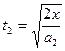由?可得?=s?-------(2分)

本题难度：简单