1、选择题  如图所示，图甲实线为方向未知的三条电场线，a、b两带电粒子从电场中的p点静止释放．不考虑两粒子间的相互作用，仅在电场力作用下，两粒子做直线运动，a、b粒子的速度大小随时间变化的关系如图乙中实线①、②所示，虚线为直线．则
（　　）
?

A．a一定带正电，b一定带负电
B．a向左运动，b向右运动
C．a电势能减小，b电势能增大
D．a动能减小，b动能增大

参考答案：A．从速度时间图象中可以看出，a粒子加速度逐渐增大，b粒子加速度逐渐减小，因为粒子仅受电场力，可知a粒子电场力逐渐增大，b粒子电场力逐渐减小，所以a 向左运动，b向右运动．由于不知电场的方向，所以无法判断a、b的电性．故A错误，B正确．
? C．带电粒子在电场中运动时，电场力做正功，所以a、b的电势能均减小．故C错误．
? D．带电粒子在电场中运动时，电场力做正功，因为仅受电场力，根据动能定理，a、b的动能均增加．故D错误．
故选B．

本题解析：

本题难度：一般

2、选择题  如图所示，足够长的传送带以恒定速率沿顺时针方向运转。现将一个物体轻轻放在传送带底端，物体第一阶段被加速到与传送带具有相同的速度，第二阶段匀速运动到传送带顶端，则下列说法中正确的是

[? ]
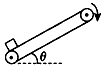
A.第一阶段和第二阶段摩擦力对物体都做正功
B.第一阶段摩擦力对物体做的功等于第一阶段物体动能的增加量
C.第二阶段摩擦力对物体做的功等于第二阶段物体机械能的增加量
D.两个阶段摩擦力对物体所做的功等于物体机械能的减少量

参考答案：AC

本题解析：

本题难度：一般

3、简答题  雪橇是一种深受青少年喜爱的雪上运动器材．在一次滑雪运动中，某同学坐在雪橇上，从静止开始沿着高度为15m的斜坡滑下，到达底部时速度为10m/s，人和雪橇的总质量为60kg．已知g=10m/s2．求：
（1）下滑过程中，合外力对人和雪橇做的功；
（2）下滑过程中，人和雪橇克服阻力做的功．

参考答案：（1）以人和雪橇整体为研究对象，对于下滑过程，根据动能定理得：
W合=12mv2t-12mv20
代入数据可得：W合=3000J；
（2）以人和雪橇整体为研究对象：W合=WG+Wf=mgh+Wf；
代入数据得：Wf=-6000J
所以，克服摩擦力做的功为6000J．
答：
（1）下滑过程中，合外力对人和雪橇做的功是3000J；
（2）下滑过程中，人和雪橇克服阻力做的功是6000J．

本题解析：

本题难度：一般

4、简答题  如图所示，有一质量为m，带电荷量为+q的小球（可视为质点），自竖直向下、场强为E的匀强电场中的P点静止下落．在P点正下方距离h处有一弹性绝缘挡板S（挡板不影响匀强电场的分布），小球每次与挡板S相碰后电荷量均减少到碰前的k倍（k＜1），而碰撞过程中小球的机械能不损失．
（1）设匀强电场中，挡板S处电势φS=0，则电场中P点的电势φP为多少？下落前小球在P点时的电势能EP为多少？
（2）小球从P点出发后到第一次速度变为零的过程中电场力对小球做了多少功？
（3）求在以后的运动过程中，小球距离挡板的最大距离l．

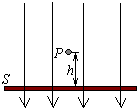
参考答案：（1）SP之间的电压为：U=Eh
因为φS=0，
φP=Eh
所以小球在P点时的电势能EP=qEh
（2）设第一次与档板碰撞后能达到的高度为h1，由能量守恒得：
mgh+qEh=（mg+kqE）h1，
从P点出发第一次到达最高点过程中电场力对小球做的功为：
W=qEh-kqEh1
解得：W=mgqEh(1-k)mg+kqE
（3）小球与挡板碰撞后小球所带电量逐渐减小，最终电量将减小为零，整个过程中能量始终守恒，由能量守恒得：
mgh+qEh=mgl
解得：l=mg+qEmgh
答：（1）设匀强电场中，挡板S处电势φS=0，则电场中P点的电势φP为Eh，下落前小球在P点时的电势能EP为qEh；
（2）小球从P点出发后到第一次速度变为零的过程中电场力对小球做的功为mgqEh(1-k)mg+kqE；
（3）求在以后的运动过程中，小球距离挡板的最大距离l为mg+qEmgh．

本题解析：

本题难度：一般

5、计算题  （10分）如图16所示，质量m=60kg的高山滑雪运动员，从A点由静止开始沿滑雪道滑下，从B点水平飞出后又落在与水平面成倾角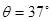的斜坡上C点。已知AB两点间的高度差为h=25m，B、C两点间的距离为s=75m，已知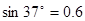，取g=10m/s2，

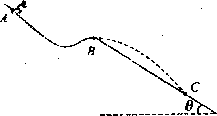
求：（1）运动员从B点水平飞出时的速度大小；
（2）运动员从A点到B点的过程中克服摩擦力做的功。

参考答案：（1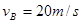）?（2）

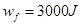
本题解析：B到C是一个平抛运动，运用平抛运动的规律解决问题，其中高度决定时间，通过水平方向运动求出初速度．
运动员从A点到B点的过程中克服摩擦力做的功，由于不清楚摩擦力的大小以及A到B得位移，从功的定义式无法求解，所以我们就应该选择动能定理．
（1）（共4分）由B到C平抛运动的时间为t
竖直方向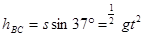：（1）?（2分）
水平方向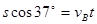：?（2）?（2分）
代得数据，解（1）（2）得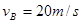?（3）?（2分）
（2）（共3分）A到B过程，由动能定理有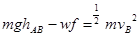?（4）?（2分）
代入数据，解（3）（4）得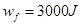?（2分）
点评：解决平抛运动的问题思路是分解，即研究水平方向的匀速直线运动和竖直方向的自由落体．动能定理的应用范围很广，可以求速度、力、功等物理量，特别是可以去求变力功．

本题难度：一般