1、简答题 如图所示,滑块A、B的质量分别为
m1与m2,m1<m2,由轻质弹簧相连接置于水平的气垫导轨上,用一轻绳把两滑块拉至最近,使弹簧处于最大压缩状态后绑紧。
两滑块一起以恒定的
速率v0向右滑动.突然轻绳断开.当弹簧伸至本身的自然长度时,滑块A的速度
正好为0.求:
小题1:绳断开到第一次恢复自然长度的过程中弹簧释放的弹性势能Ep;
小题2:在以后的运动过程中,滑块B是否会有速度为0的时刻?试通过定量分析证明你的结论.
参考答案:
小题1:Ep=(m1-m2)(m1+m2)v02/2m2.
小题2:不可能
本题解析:
小题1:当弹簧处压缩状态时,系统的机械能等于两滑块的动能和弹簧的弹性势能之和,当弹簧伸长到自然长度时,弹性势能为0,因这时滑块A的速度为0,故 系统的机械能等于滑块B的动能.设这时滑块B的速度为v,则有E=m2v2/2.
因系统所受外力为0,由动量守恒定律
(m1+m2)v0=m2v.
解得E=(m1+m2)2v02/(2m2).
由于只有弹簧的弹力做功,系统的机械能守恒
(m1+m2)v02/2+Ep=E.
解得Ep=(m1-m2)(m1+m2)v02/2m2.
小题2:假设在以后的运动中滑块B可以出现速度为0的时刻,并设此时A的速度为v1,弹簧的弹性势能为E′p,由机械能守恒定律得
m1v12/2+E′p=(m1+m2)2v02/2m2.
根据动量守恒得(m1+m2)v0=m1v1,
求出v1代入上式得:
(m1+m2)2v02/2m1+E′p=(m1+m2)2v02/2m2.
因为E′p≥0,故得:
(m1+m2)2v02/2m1≤(m1+m2)2v02/2m2
即m1≥m2,这与已知条件中m1<m2不符.
可见在以后的运动中不可能出现滑块B的速度为0的情况.
本题难度:一般
2、选择题 不定项选择
如图,斜面体C质量为M,足够长,始终静止在水平面上,一质量为m的长方形木板A上表面光滑,木板A获得初速度v0后恰好能沿斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木板A表面上,当滑块B在木板A上滑动时,下列说法正确的是( ? )
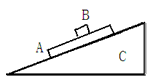
A.滑块B的动量为0.5mv0时,木板A和滑块B的加速度大小相等
B.滑块B的动量为0.5mv0时,斜面体对水平面的压力大小为(M+2m)g
C.滑块B的动量为1.5mv0时,木板A的动量为0.5mv0
D.滑块B的动量为1.5mv0时,水平面对斜面体的摩擦力向右
参考答案:AB
本题解析:
本题难度:一般
3、计算题 如图,一块平板P2置于光滑水平面上,质量为2m,其右端固定轻质弹簧,左端放置一个物体P1,质量为m可看作质点。平板P2上弹簧的自由端离物体P1相距为L的部分是粗糙的,其余部分是光滑,且P1与P2之间的动摩擦因数为μ 。现有一颗子弹P质量为 以速度
以速度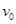 水平向右打入物体P1并留在其中,子弹打入过程时间极短。随后的运动过程中,(重力加速度为g)求
水平向右打入物体P1并留在其中,子弹打入过程时间极短。随后的运动过程中,(重力加速度为g)求
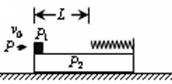
(1)子弹P打入物体P1后的共同速度v1
(2)若子弹P与物体P1最终能停在平板P2的最左端,则L至少为多少?
(3)试讨论动摩擦因数为μ与此过程中弹簧的最大弹性势能EP的关系
参考答案:(1) 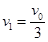 ?(2)
?(2)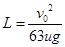 (3)若u>=
(3)若u>=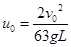 时,Ep=0?若u<
时,Ep=0?若u<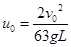 时,
时,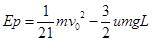
本题解析: (1)子弹P打入物体P1后的共同速度v1,根据动量守恒定律可得
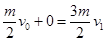 ,即
,即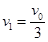
(2)到最后若子弹P与物体P1最终能停在平板P2的最左端,则最终所有物体的速度相同,由于在整个装置中,系统总合外力为零,设最终速度为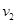 ,则
,则
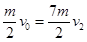
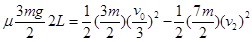
求得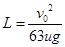
(3)若u>=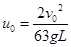 时,则可能在为碰到弹簧前就已经与P2达到共同速度,即Ep=0?
时,则可能在为碰到弹簧前就已经与P2达到共同速度,即Ep=0?
若u<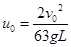 时,则当两者速度相等时,弹簧弹性势能最大,根据
时,则当两者速度相等时,弹簧弹性势能最大,根据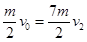 可知达到共同速度为
可知达到共同速度为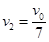 ,弹性势能为
,弹性势能为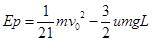
点评:本题考查了较为复杂的系统动量守恒的分析,在整个装置中,系统合外力为零,因此系统不论何时动量总是守恒。
本题难度:一般
4、简答题 如图1-5-9所示,质量为M的金属圆环,半径为R,竖直放在光滑水平面上,质量为m的小球从与圆心等高的位置沿圆环内侧滚下,求小球滚到圆环最低点时的水平位移为多少?
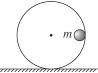
图1-5-9
参考答案: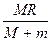
本题解析:据题意可画出草图,如下图所示,设小球的水平位移为s1,环的水平位移为s2,系统水平方向上动量守恒,可列方程求解.
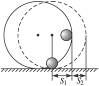
由动量守恒可知:ms1=Ms2,s1+s2=R
解得:s1=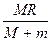 .
.
本题难度:简单
5、选择题 如图所示,两根位于同一竖直平面内的水平长杆,上、下两杆上分别套着质量相等的甲、乙两金属球,两球之间用一轻质弹簧相连。开始时乙在甲的正下方,且弹簧刚好无弹力。现给甲一个水平向右的初速度v0,此后两球在杆上无摩擦地滑动。下列叙述中正确的是
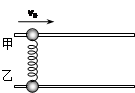
A.甲、乙两球加速度始终相同
B.甲、乙两球的动能之和保持不变
C.当甲球的速度为零时,乙球刚好位于甲球的正下方
D.甲球的速度减小至零的过程中,弹簧的弹性势能先增大后减小
参考答案:CD
本题解析:弹簧伸长以后,甲向右做减速运动,乙向右做加速运动,加速度方向不同,但加速度大小相等,A错;根据能量守恒定律两球的动能减小量转化为弹簧的弹性势能,B错;甲乙两小球水平方向不受外力,动量守恒,整个系统无机械能损失,机械能守恒,由两个守恒公式可以判断,当甲球速度为零时,乙球获得速度为v0,弹簧为原长位置,C对;当两球速度相同时系统损失动能最多,弹簧弹性势能最大,D对;
本题难度:简单
He who commences many things finishes but few. 样样都搞, 完成者少.