1、计算题  如图所示，长为L=9m的传送带与水平方向的倾角θ=37°，在电动机的带动下以v=4m/s的速率沿顺时针方向运行，在传送带的B端有一离传送带很近的挡板P可将传送带上的物体挡住，在传送带的A端无初速度地释放一质量m=1Kg的物体，它与传送带之间的动摩擦因数为0.5，物体与挡板碰撞时的能量损失及碰撞时间均不计。（sin37°=0.6，cos37°=0.8）

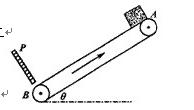
①在物体从第一次由静止开始下滑到与挡板P第一次相碰后，物体再次上升到最高点的过程中，由于摩擦而产生的热量为多少？
②试求物体最终的运动状态以及达到该运动状态后电动机的输出功率P。

参考答案：（1）100.8J?（2）最终物块在P与离P 4m的范围内不断做向上的加速度为2 m/s2的减速运动和向下做加速度为2 m/s2的加速运动? 16w

本题解析：（1）物块从A点由静止释放，物块相对传送带向下滑，物块沿传送带向下加速运动的加速度?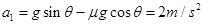
与P碰前的速度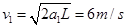
物块从A到B的时间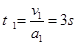
在此过程中物块相对传送带向下位移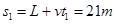
挡板碰撞后，以v1的速度反弹，因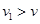，物块相对传送带向上滑，物块向上做减速运动的加速度为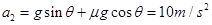
物块速度减小到与传送带速度相等的时间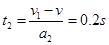
在t2时间内物块向上的位移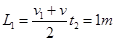
物块相对传送带向上的位移?
与传送带速度相等后物块相对传送带向下滑，物块向上做减速运动的加速度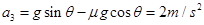
物块速度减小到零的时间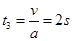
物块向上的位移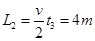
此过程中物块相对传送带向下的位移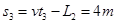
摩擦生热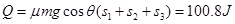
（2）物块块上升到传送带的最高点后，物块沿传送带向下加速运动，与挡板P第二次碰掸前的速度
碰后因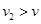，物块先向上做加速度为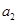的减速运动，再做加速度为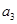?的减速运动，物块向上的位移为
物块与挡板第三次碰撞前的速度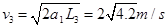
在此类推经过多次碰撞后物块以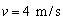的速度反弹，故最终物块在P与离P 4m的范围内不断做向上的加速度为2 m/s2的减速运动和向下做加速度为2 m/s2的加速运动，物块的运动达到这一稳定状态后，物块对传送带有一与传送带运动方向相反的阻力（分析过程酌情给分）

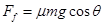
输出功率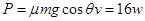

本题难度：一般

2、选择题  一质点沿直线Ox方向做变速运动，它离开O点的距离随时间变化的关系为x=5+2t3（m），它的速度随时间t变化的关系为v=6t2（m/s）．该质点在t=0到t=2s间的平均速度和t=2s到t=3s间的平均速度大小分别为（　　）
A．12?m/s，39?m/s
B．8?m/s，38?m/s
C．12?m/s，19.5?m/s
D．8?m/s，12?m/s

参考答案：根据质点离开O点的距离随时间变化的关系为x=5+2t3（m）得当：
t=0时，x0=5m；
t=2s时，x2=21m
t=3s时，x3=59m
则质点在t=0到t=2s时间内的位移△x1=x2-x1=16m，.v=△x1△t1=8m/s
则质点在t=2s到t=3s时间内的位移△x3=x3-x2=38m，.v2=△x3△t2=38m/s
故选B．

本题解析：

本题难度：一般

3、简答题  某辆汽车从静止开始做匀加速直线运动，加速度大小为0.5m/s2，达到30m/s时，突然发现前方有障碍物，便立即制动，做匀减速直线运动的加速度为3m/s2．求：
（1）汽车由启动至停下来全过程的运动时间为多少？
（2）全运动过程的位移为多少？

参考答案：（1）加速时间t1=va1=300.5=60s
减速时间t2=va2=303=10s
全过程运动时间t总=t1+t2=70s
（2）加速位移S1=vt12=30×602=900m
减速位移S2=vt22=30×102=150m
全程总位移S=S1+S2=1050m．
答：（1）汽车由启动至停下来全过程的运动时间为70s．（2）全运动过程的位移为1050m．

本题解析：

本题难度：一般

4、简答题  如图所示，质量M=1.0kg，长L=l．0m的木板静止在粗糙的水平地面上，木板与地面间的动摩擦因数μ1=0.1kg．在木板的左端放置一个质量m=1.0kg、大小可以忽略的铁块，铁块与木板间的动摩擦因数μ2=0.4．认为最大静摩擦力等于滑动摩擦力，取g=10m/s2．若在铁块上加一个水平向右的恒力F=8.0N，求：
（1）铁块的加速度的大小是多少？
（2）木板的加速度的大小是多少？
（3）经过多长时间铁块运动到木板的右端？

参考答案：（1）对于铁块，由牛顿第二定律得：
F-μ2mg=ma1
解得a1=4m/s2．
（2）对于木板，由牛顿第二定律得：
μ2mg-μ1（m+M）g=Ma2
解得a2=2m/s2．
（3）设铁块运动到木板的右端的时间为t，则：
铁块的位移为：s1=12a1t2
木板的位移为：s2=12a2t2
当铁块运动到木板右端时，有：L=s1-s2
联立三式解得：t=1s．
答：（1）铁块的加速度的大小是4m/s2．
（2）木板的加速度的大小为2m/s2．
（3）经过1s铁块运动到木板的右端．

本题解析：

本题难度：一般

5、计算题  为了缩短下楼的时间,消防员往往抱着楼房外的竖直杆直接滑下,设消防员先做自由落体运动,再以可能的最大加速度沿杆做匀减速直线运动．一名质量m=65kg的消防员,在沿竖直杆无初速度滑至地面的过程中,重心共下降了h=11.4m,该消防员与杆之间的滑动摩擦力最大可达到fm=975N,消防员着地的速度不能超过v=6m/s．(g=10m/s2)求:
(1)消防员下滑过程中速度的最大值；
(2)消防员下滑过程的最短时间。

参考答案：解：(1)消防队员抱着竖直杆做自由落体运动时,设消防员下滑过程中速度的最大值为vm
则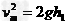
对消防员匀减速直线运动,设最大加速度的大小为a
则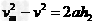
由牛顿第二定律得:

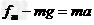
a=5m/s2
由题意:

联立解得:vm＝10m/s
(2)对消防员自由下落:
所以t1=1.0s
对消防员匀减速直线运动:
所以t2=0.8s
故消防员下滑过程的最短时间:
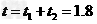s

本题解析：

本题难度：一般