1、选择题  如图所示，虚线间空间存在由匀强电场E和匀强磁场B组成的正交或平行的电场和磁场（实线为电场线），有一个带正电小球（电量为+q，质量为m）从正交或平行的电磁混合场上方的某一高度自由落下，那么，带电小球可能沿直线通过下列的哪些电磁混合场（　　）
A．

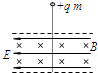
B．

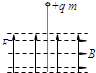
C．

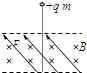
D．

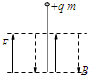
参考答案：A、小球受重力、向左的电场力、向右的洛伦兹力，下降过程中速度一定变大，故洛伦兹力一定变化，不可能一直与电场力平衡，故合力不可能一直向下，故一定做曲线运动，故A错误；
B、小球受重力、向左的电场力、垂直向外的洛伦兹力，合力与速度一定不共线，故一定做曲线运动，故B错误；
C、小球受重力、向左上方的电场力、水平向右的洛伦兹力，若三力平衡，则粒子做匀速直线运动，故C正确；
D、粒子受向下的重力和向上的洛伦兹力，合力一定与速度共线，故粒子一定做直线运动，故D正确；
故选CD．

本题解析：

本题难度：一般

2、计算题  如图12所示，一个半径为R的绝缘光滑半圆环，竖直放在场强为E的匀强电场中，电场方向竖直向下．在环壁边缘处有一质量为m，带有正电荷q的小球，由静止开始下滑，求小球经过最低点时对环底的压力．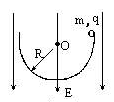

参考答案：3（mg＋qE）

本题解析：在最低点小球受到竖直向下的重力和电场力，以及竖直向上的支持力，故根据牛顿第二定律可得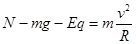
过程中只有重力和电场力做功，所以根据动能定理可得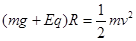
两式联立可得
点评：本题关键是抓住功能关系的不同表现形式进行分析，其中动能定理是功能关系中最常用的一条规律，机械能守恒的条件是除重力外其余力不做功．

本题难度：简单

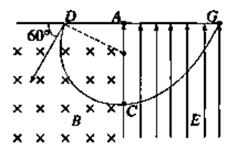
3、计算题  如右图所示，一个质量为m、电荷量为q的正离子，从D处沿图示方向以一定的速度射入磁感应强度为B的匀强磁场中，磁场方向垂直纸面向里．结果离子正好从距A点为d的小孔C沿垂直于电场方向进入匀强电场，此电场方向与AC平行且向上，最后离子打在距离A点2d的G处， AG⊥AC．若不计离子重力，离子运动轨迹始终在纸面内，试求：

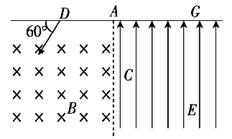
⑴此离子在磁场中做圆周运动的半径r；
⑵离子从D处运动到G处所需时间；
⑶离子到达G处时的动能．

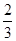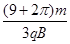参考答案：(1)d (2)?(3)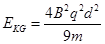

本题解析：（1）正离子的运动轨迹如图所示，离子圆周运动半径r满足：
r+rcos 60°=d　
解得：r=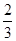d　

（2）设离子在磁场中运动的速度为v0，则有

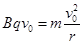
得，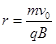
离子在磁场中运动的周期为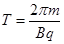
根据轨迹得：离子在磁场中做圆周运动的时间为：
，
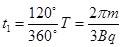离子从C运动到G做类平抛运动，水平方向做匀速直线运动，所需的时间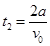
由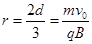
得，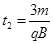
故离子从D→C→G的总时间为：
t=t1+t2=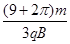
（2）设电场强度为E，对离子在电场中的运动过程，有：
qE=ma，d=at22　
由动能定理得：Eq?d=EkG-mv02　
解得：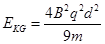

本题难度：一般

4、选择题  如图所示，在同时存在匀强磁场和匀强电场的空间中取正交坐标系Oxyz(z轴正方向竖直向上)，一质量为m、电荷量为q的带正电粒子(重力不能忽略)从原点O以速度v沿y轴正方向出发．下列说法正确的是?

[? ]
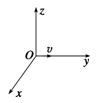
A．若电场沿z轴正方向、磁场沿y轴正方向，粒子只能做曲线运动
B．若电场沿z轴正方向，磁场沿z轴正方向，粒子有可能做匀速圆周运动
C．若电场沿x轴正方向、磁场沿z轴正方向，粒子有可能做匀速直线运动
D．若电场沿x轴正方向、磁场沿x轴负方向，粒子有可能做匀速圆周运动

参考答案：B

本题解析：

本题难度：一般

5、计算题  光滑的平行金属导轨长L＝2 m，两导轨间距d＝0.5 m，轨道平面与水平面的夹角θ＝30°，导轨上端接一阻值为R＝0.6 Ω的电阻，轨道所在空间有垂直轨道平面向上的匀强磁场，磁场的磁感应强度B＝1 T，如图所示．有一质量m＝0.5 kg、电阻r＝0.4 Ω的金属棒ab，放在导轨最上端，其余部分电阻不计．已知棒ab从轨道最上端由静止开始下滑到最底端脱离轨道的过程中，电阻R上产生的热量Q1＝0.6 J，取g＝10 m/s2，试求：

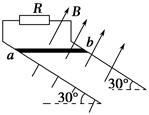
(1)当棒的速度v＝2 m/s时，电阻R两端的电压；
(2)棒下滑到轨道最底端时速度的大小；
(3)棒下滑到轨道最底端时加速度a的大小．

参考答案：(1) 0.6 V (2) 4 m/s (3) 3 m/s2.

本题解析：(1)当棒的速度v＝2 m/s时，棒中产生的感应电动势E＝Bdv＝1 V
此时电路中的电流I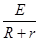＝＝1 A，所以电阻R两端的电压U＝IR＝0.6 V.
(2)根据Q＝I2Rt得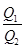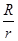＝，可知在棒下滑的整个过程中金属棒中产生的热量Q2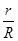＝Q1＝0.4 J
设棒到达最底端时的速度为v2，根据能的转化和守恒定律，有：mgLsin θ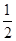＝mv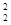＋Q1＋Q2，解得：v2＝4 m/s.
(3)棒到达最底端时回路中产生的感应电流I2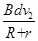＝＝2 A
根据牛顿第二定律有：mgsin θ－BI2d＝ma，解得：a＝3 m/s2.
点评：在金属棒切割磁感线产生感应电动势的过程中，注意当金属棒运动的速度方向与磁场方向不垂直时，把速度分解为平行于磁场方向和垂直于磁场方向，只有垂直方向的分速度切割磁场产生电动势．

本题难度：一般