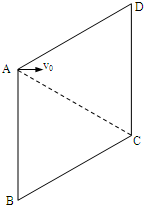
1、简答题  由二个边长为L的正三角形组成的菱形区域内存在匀强电场，电场方向平行于AB、由B指向A．现有一电子垂直于AB边从A点射入电场，射入的速度为v0，电子恰从C点射出．已知电子质量为m，电荷量为-q．
（1）求电场强度的大小；
（2）若电子射入电场，经过时间t1=

参考答案：（1）电子垂直于AB边从A点射入电场，从C点射出，
垂直AB方向：

本题解析：

本题难度：一般

2、选择题  下列关于匀强电场中场强和电势差的关系的说法中不正确的是
[? ]
A．在相同的距离上，电势差大的其场强也必定大
B．任意两点的电势差，等于场强与这两点间距离的乘积
C．电势降低的方向，必定是电场强度的方向
D．沿着电场线方向，相等距离上的电势降落必定相等

参考答案：ABC

本题解析：

本题难度：一般

3、简答题  如图所示，一个绝缘光滑圆环竖直放在水平向右的匀强电场中，圆环半径大小为R=1.0m，电场强度大小为E=6.0×106V/m，现将一小物块由与圆心O等高的位置A点静止释放，已知小物块质量为m=1.6kg，电荷量为q=+2.0×10-6C，释放后滑块将沿着圆环滑动．小物块可视为质点，g取10m/s2．求：
（1）当物块滑到圆环最低点B时对轨道的压力大小；
（2）若在圆环最低点B点给小物块一个水平向左的初速度vB=9m/s，那么物块能否紧贴圆环在竖直平面内做圆周运动．（写出详细分析、判定过程）（已知：sin37°=0.6；cos37°=0.8）

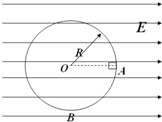
参考答案：（1）物块由A运动到B的过程中，重力做正功，电场力做负功．
由动能定理可得：mgR+(-qER)=12mv2B
解得：v2B=2gR-2qERm=2×10×1.0-2×2.0×10-6×6.0×106×1.01.6=5（m/s）2
在B点由 FN-mg=mv2BR
解得：FN=mv2BR+mg=1.6×（51.0+10）N=24N
由牛顿第三定律可得物块对轨道的压力大小为：F′N=24N
（2）设在C位置时重力与电场力的合力恰好指向圆心提供物块做圆周运动向心力时，物块刚好脱离圆环．
此时有：

本题解析：

本题难度：一般

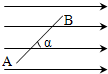
4、选择题  如图所示，匀强电场的场强E=3×105V/m，A、B两点相距0.2m，两点连线与电场的夹角是60°，下列说法正确的是（　　）
A．A、B两点间的电势差是U=6×104V
B．若取A点的电势为0，则B点的电势φB=3×104V
C．电荷量q=+2×10-4C的电荷从A点运动到B点电势能增加6J
D．电荷量q=-2×10-4C的电荷从A点运动到B点电场力做功为-6J