1、简答题  如图，半径R=0.4m光滑半圆环轨道处在竖直平面内，半圆环与粗糙在水平地面相切于圆环的端点A．一质量m=0.1Kg的小球以初速v0=7m/s在水平地面上向左做加速度a=3m/s2的匀减速直线运动，运动x=4m后，冲竖直半圆环，最后小球落在C点．（取g=10m/s2）．求
（1）小球运动到A处时的速度．
（2）小球能否到达轨道最高点B，不能请说明理由，若能则求出在B点时小球的速度．
（3）求AC间的距离．

参考答案：（1）小球在水平地面向左匀减速运动4m的过程中，有：
vA2-v02=2as
解得：vA=5m/s
（2）假设小球能够通过最高点B，从A到B的过程运用动能定理得：
12mvB2-12mvA2=2mgR
解得：vB=3m/s
小球恰好能到最高点B应满足：mg=mvm2R
解得：vm=2m/s
因为vB＞vm
所以能通过最高点B．
（3）小球从B点抛出后做平抛运动，有2R=12gt2
解得：t=0.4s
xAC=vBt=1.2m
答：（1）小球运动到A处时的速度为5m/s；（2）小球能到达轨道最高点B，B点的速度为3m/s；（3）AC间的距离为1.2m．

本题解析：

本题难度：一般

2、简答题  如图所示，平行金属带电极板A、B间可看作匀强电场，场强E=1.2×103V/m，极板间距离d=5cm，电场中C和D分别到A、B两板距离均为0.5cm，B板接地，求：
（1）C和D两点的电势、两点间的电势差UCD；
（2）点电荷q1=-2×10-3C分别在C和D两点的电势能；
（3）将点电荷q2=2×10-3C从C匀速移到D时除电场力以外的力做功多少？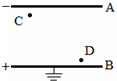

参考答案：

本题解析：

本题难度：一般

3、简答题  如图甲所示，一足够长、与水平面夹角θ=53°的倾斜轨道与竖直面内的光滑圆轨道相接，圆轨道的半径为R，其最低点为A，最高点为B．可视为质点的物块与斜轨间有摩擦，物块从斜轨上某处由静止释放，到达B点时与轨道间压力的大小F与释放的位置距最低点的高度h的关系图象如图乙所示，不计小球通过A点时的能量损失，重力加速度g=10m/s2，sin53°=

参考答案：（1）由乙图可知，当h1=5R时，物块到达B点时与轨道间压力的大小为0，设此时物块在B点的速度大小为v1，则：mg=mv2R
对物块从释放至到达B点过程，由动能定理得：mg(h1-2R)-μmgcosθh1sinθ=12mv21
解得：μ=23
（2）设物块从距最低点高为h处释放后到达B点时速度的大小为v，则：F+mg=mv2?R
对物块从释放至到达B点过程，由动能定理得：mg(h?-2R)-μmgcosθhsinθ=12mv2?
解得：F=mghR-5mg
则F-h图线的斜率：k=mgR
由乙图可知：k=2R
解得：m=0.2kg
答：（1）物块与斜轨间的动摩擦因数μ为23；
（2）物块的质量m是0.2kg．

本题解析：

本题难度：一般

4、简答题  如图，质量m=4.0kg的物体在恒力F=40N作用下，由静止开始沿水平面运动x=2.0m，力F与水方向的夹角α=37°，物体与水平面间的动摩擦因数μ=0.5，求该过程中：
（sin37°=0.6，cos37°=0.8，g=10m/s2）
（1）地面对物体的摩擦力Ff的大小；
（2）物体获得的动能Ek．

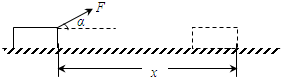
参考答案：（1）由平衡条件得：Fsin37°+FN=mg，
物体受到的滑动摩擦力f=μFN，解得：f=8N．
（2）以物体为研究对象，由动能定理可得：
Fxcos37°-fx=Ek-0，解得：Ek=48J；
答：（1）地面对物体的摩擦力的大小为8N．
（2）物体获得的动能为48J．

本题解析：

本题难度：一般

5、选择题  一杂技演员表演单手连续竖直抛鸡蛋(另一手接、递鸡蛋)，为了增加表演的惊险度，他使鸡蛋能达到他头顶上方50cm处，则他在抛出一只鸡蛋的过程中所做的功最接近于
A．0.06J
B．0.6J
C．6J
D．60J

参考答案：B

本题解析：鸡蛋重力接近1N，抛出时人做功转化成重力势能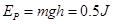，，最接近B.

本题难度：简单