1、计算题  如图所示，在xOy平面内，紧挨着的三个“柳叶”形有界区域①②③内（含边界上）有磁感应强度为B的匀强磁场，它们的边界都是半径为a的l/4圆，每个1／4圆的端点处的切线要么与x轴平行、要么与y轴平行．①区域的下端恰在O点，①②区域在A点平滑连接、②③区域在C点平滑连接：大量质量均为m，电荷量均为q的带正电的粒子依次从坐标原点。以相同的速率、各种不同的方向射入第一象限内（含沿x’轴、y轴方向），它们只要在磁场中运动，轨道半径就都为a，在y≤—a的区域，存在场强为E的沿一x方向的匀强电场．整个装置在真空中．不计粒子重力、不计粒子之间的相互作用．求：?
（1）粒子从O点出射时的速率v0；
（2）这群粒子中，从P点射出至运动到x轴上的最长时间；
（3）这群粒子到达y轴上的区域范围．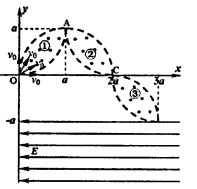

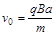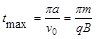参考答案：（1）（2）（3）

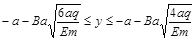
本题解析：（1）由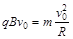得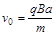
（2）这些粒子中，从O沿+y轴方向射入磁场的粒子，从O到C耗时最长

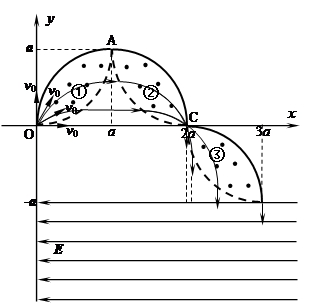
由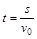得?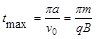
（3）这些粒子经过①区域偏转后方向都变成与 +x轴平行；接着匀速直线进入②区域，经过②区域偏转又都通过C点；
从C点进入③区域，经过③区域偏转，离开③区域时，所有粒子都变成与－y轴平行（即垂直进入电场）
对于从x = 2a进入电场的粒子，在－x方向的分运动有：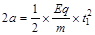
解得?
则该粒子运动到y轴上的坐标为

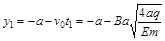
对于从x = 3a进入电场的粒子，在－x方向的分运动有：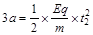
解得?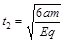
则该粒子运动到y轴上的坐标为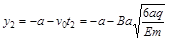
这群粒子运动到y轴上的区间为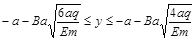

本题难度：一般

2、计算题  为了测定带电粒子的比荷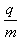，让这个带电粒子垂直电场方向飞进平行金属板间，已知匀强电场的场强为E，在通过长为L的两金属板间后，测得偏离入射方向的距离为d，如果在两板间加垂直电场方向的匀强磁场，磁场方向垂直于粒子的入射方向，磁感应强度为B，则粒子恰好不偏离原来方向，求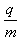为多少？

参考答案：解：仅加电场时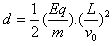
加复合场时Bqv0=Eq
由以上两式可得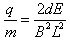

本题解析：

本题难度：一般

3、填空题  ?将带等量异种电荷的两金属板相隔一定距离，水平放置在方向竖直向下的匀强磁场中，将一个带正电的微粒以初速度v0垂直极板自下极板的小孔射入板间，未到达上极板，又从下极板小孔射出，如图，不计微粒重力，则(? )

A?只减小磁感应强度，可能使微粒到达上极板。
B?只减小板间距，可能使微粒到达上极板。
C?只错开极板正对面积，(微粒仍处在电场内)可能使微粒到达上极板。
D?只减少微粒带电量，可能使微粒到达上极板。

参考答案：BD

本题解析：因磁场的方向与微粒的运动在同一直线上，所以磁场对微粒的运动不产生影响，可不予考虑。即A项错误；只减小板间距离，由于板上的电荷密集程度不变，所以内部电场强度也不变，微粒所受电场力不变，所以则动能定理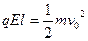可知，微粒运动的距离增大，有可能使微粒到达上极板，所以B项正确；只错开极板的正对面积，使得极板上的电荷密集程度变大，所以内总电场强度增大，由上式可知，微粒的运动距离减小，所以微粒一定不能到达上极板，所以C项错误；由上式可知，减小微粒的带电量，可增大微粒的运动距离，有可能使微粒到达上极板。所以D项正确。

本题难度：一般

4、简答题  一个质量为m，带电量为+q的粒子，以速度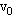沿水平方向从如图所示的小孔M进入垂直于纸面的匀强磁场区域Ⅰ，并从小孔N沿竖直向上的方向进入到有水平方向匀强电场区域Ⅱ，最后打在P点，且OM=OP=d，重力不计．

(1)求区域Ⅰ中磁感强度的大小，粒子从M运动到N所用时间．并在图上标出磁场的方向．
(2)求区域Ⅱ中电场强度的大小，粒子从小孔N运动到P所用时间，并在图上标出电场方向．
(3)求粒子到达P点的速度大小．

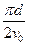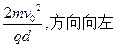参考答案：（1）??（2）?(3)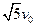

本题解析：

本题难度：一般

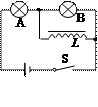
5、选择题  如图9所示电路中，L为电感线圈，电阻不计，A、B为两灯泡，则

参考答案：BCD

本题解析：略

本题难度：简单