1、实验题 如图15-2-16所示,水平放置的光滑金属导轨M、N,平行地置于匀强磁场中,间距为d,磁场的磁感应强度大小为B,方向与导轨平面夹角为α.金属棒ab的质量为m,放在导轨上且与导轨垂直,电源电动势为E,定值电阻为R,其余部分电阻不计.则当电键K合上时,棒ab受到的安培力的大小为_____________,方向为_____________,棒的加速度大小为_____________.
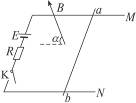
图15-2-16
参考答案:BEd/R?左下方? EBdsinα/mR
本题解析:F="BIL?" I=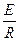 ,L=d,F=
,L=d,F=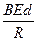 ,由左手定则可知安培力方向沿左下方
,由左手定则可知安培力方向沿左下方
a=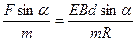 .
.
本题难度:简单
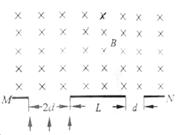
2、选择题 利用如图所示装置可以选择一定速度范围内的带电粒子。图中板MN上方是磁感应强度大小为B、方向垂直纸面向里的匀强磁场,板上有两条宽度分别为2d和d的缝,两缝近端相距为L。一群质量为m、电荷量为q,具有不同速度的粒子从宽度为2d的缝垂直于板MN进入磁场,对于能够从宽度为d的缝射出的粒子,下列说法正确的是( )
A. 粒子带正电
B. 射出粒子的最大速度为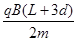
C. 保持d和L不变,增大B,射出粒子的最大速度与最小速度之差增大
D. 保持d和B不变,增大L,射出粒子的最大速度与最小速度之差增大
参考答案:BC
本题解析:不同速度的粒子从宽度为2d的缝垂直于板MN进入磁场向右偏,所以根据左手定则可判断粒子带负电,故A错误;当粒子从2d的缝的最左端进入,从宽为d的缝的最右端射出时,粒子的最大半径,为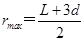 、,从2d缝的最右端进,而从d缝的最左端出时,粒子的最小半径,为
、,从2d缝的最右端进,而从d缝的最左端出时,粒子的最小半径,为 ,根据
,根据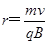 ,可得
,可得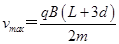 、
、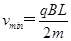 ,则
,则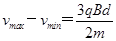 ,与L大小无关,故可知BC正确。
,与L大小无关,故可知BC正确。
本题难度:一般
3、选择题 如图所示R为某种天然放射性元素,R发出的射线沿RO方向射出,虚线框内有垂直于线框平面的匀强磁场,PQ是厚纸板,MN是荧光屏,实验时发现屏上O、A两处有亮斑,下面判断正确的是(?)

A.磁场方向垂直线框向内,到达O点的是中子
B.磁场方向垂直线框向内,到达A点的是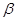 粒子
粒子
C.增强磁场有可能使A处亮斑消失
D.增强磁场有可能在O点之上新增一个亮斑
参考答案:BC
本题解析:放射性元素能放出  三种射线,而
三种射线,而 射线不能穿过厚纸板,所以穿过厚纸板的只有
射线不能穿过厚纸板,所以穿过厚纸板的只有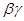 两种射线,因为
两种射线,因为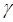 是光子流,不带电,所以在磁场中不偏转,所以到达O点的是
是光子流,不带电,所以在磁场中不偏转,所以到达O点的是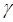 光子;磁场方向垂直线框向内,,则
光子;磁场方向垂直线框向内,,则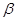 粒子受向下的洛伦兹力,所以到达A点的是
粒子受向下的洛伦兹力,所以到达A点的是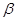 粒子;增强磁场则可能使得
粒子;增强磁场则可能使得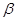 粒子偏转角度过大而使其打不到屏上从而使A处亮斑消失,但不可能在O点之上新增一个亮斑,选项BC正确。
粒子偏转角度过大而使其打不到屏上从而使A处亮斑消失,但不可能在O点之上新增一个亮斑,选项BC正确。 三种射线及其性质。
三种射线及其性质。
本题难度:一般
4、选择题 如图所示,A板发出的电子(重力不计)经加速后,水平射入水平放置的两平行金属板M、N间,M、N之间有垂直纸面向里的匀强磁场,电子通过磁场后最终打在荧光屏P上,关于电子的运动,下列说法中正确的是
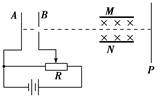
A.当滑动触头向右移动时,电子打在荧光屏的位置上升
B.当滑动触头向右移动时,电子通过磁场区域所用时间不变
C.若磁场的磁感应强度增大,则电子打在荧光屏上的速度大小不变
D.若磁场的磁感应强度增大,则电子打在荧光屏上的速度变大
参考答案:AC
本题解析:当滑动触头向右移动时,电场的加速电压增大,加速后动能增大,进入磁场的初速度增大,向下偏转程度变小,位置上升,选项A正确。由于在磁场中运动对应的圆心角变小,运动时间变短,选项B错误。粒子在磁场中运动速度大小不变,选项C正确、D错误。
本题难度:一般
5、选择题 如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹θ角.则正、负离子在磁场中:
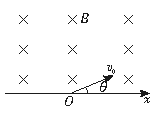
A.运动时间相同
B.运动轨道半径相同
C.重新回到x轴时速度大小和方向均相同
D.重新回到x轴时距O点的距离相同
参考答案:BCD
本题解析:分析:正负离子垂直射入磁场后都做匀速圆周运动,根据牛顿第二定律研究轨道半径关系.根据圆的对称性分析重新回到磁场边界时正负离子速度大小和方向的关系.写出轨迹的圆心角,研究运动的时间关系.根据几何知识研究正负离子重新回到磁场边界的位置与O点距离关系.
解答:解:A、设正离子轨迹的圆心角为α,负离子轨迹的圆心角为β.由几何知识得到,α=2π-2θ,β=2θ,正离子运动的时间为t1=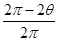 T,正离子运动的时间为t2=
T,正离子运动的时间为t2=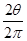 T,而周期T=
T,而周期T=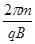 相同,则t1>t2.故A错误.
相同,则t1>t2.故A错误.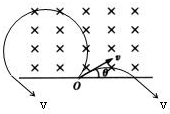
B、正负离子垂直射入磁场后都做匀速圆周运动的半径为r=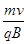 ,由题意可知,正负离子质量、电荷量均相等,速度相同,B相同,则它们运动的轨道半径相同.故B正确.
,由题意可知,正负离子质量、电荷量均相等,速度相同,B相同,则它们运动的轨道半径相同.故B正确.
C、两个离子轨迹都是圆,速度是轨迹的切线方向,如图,根据圆的对称性可知,重新回到磁场边界时速度大小和方向都相同.故C错误.
D、根据几何知识得到,重新回到磁场边界的位置与O点距离相等.故D正确.
故选BCD
点评:带电粒子垂直射入单边界的匀强磁场中,可分两类模型分析:一为同方向射入的不同粒子;二为同种粒子以相同的速率沿不同方向射入.无论哪类模型,都遵守以下规律:
(1)轨迹的圆心在入射方向的垂直线上,常可通过此垂线的交点确定圆心的位置.
(2)粒子射出方向与边界的夹角等于射入方向与边界的夹角.
本题难度:简单