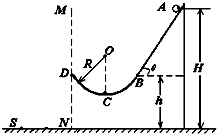
1、简答题  2006年都灵冬奥会上，我国选手以总分250.77的成绩创造中国自由式滑雪的里程碑，实现了我国冬奥史上金牌两个“零的突破”（男子项目金牌零的突破和雪上项目金牌零的突破），创造了我国冬奥会历史上的奇迹．自由式滑雪的运动模型可简化如下：如图所示，斜面轨道AB与水平面之间的夹角θ=53°，BD为半径R=4m的圆弧形轨道，且B点与D点在同一水平面上，在B点，轨道AB与圆弧形轨道BD相切，整个轨道处于竖直平面内且处处光滑，在A点处的一质量m=1kg的小球由静止滑下，经过B、C点后从D点斜抛出去，最后落在地面上的S点处时的速度大小vs=8m/s，已知A点距地面的高度H=10m，B点距地面的高度h=5m，设以MDN为分界线，假设其左边为存在空气阻力的区域，右边为不考虑空气阻力的真空区域，g取10m/s2，cos53°=0.6
（1）小球经过B点的速度为多大？
（2）小球经过圆弧轨道最低处C点时对轨道的压力多大？
（3）小球从D点抛出后，在MDN分界线左边的区域受到的阻力f与其瞬时速度方向始终相反，求小球从D点至S点的过程中，阻力f所做的功．

参考答案：（1）从A到B过程中，由动能定理得：
mg（H-h）=12mvB2-0，
解得：vB=

本题解析：

本题难度：一般

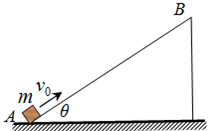
2、简答题  质量m=2kg的物块自斜面底端A以初速度v0=10m/s沿足够长的固定斜面向上滑行，经时间t=1s速度减为零．已知斜面的倾角θ=37°，重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8．试求：
（1）物块上滑过程中加速度的大小；
（2）物块上滑过程中克服摩擦力做的功；
（3）物块回到底端A时的动能．

参考答案：（1）物体的加速度：
a=△v△t=0-101=-10m/s2；
加速度的大小a=10m/s2；
（2）物块上滑过程中的最大位移：x=v0+02t=5m，
由牛顿第二定律得：mgsinθ+μmgcosθ=ma，
解得，摩擦力：Ff=μmgcosθ=ma-mgsinθ=8N，
物块克服摩擦力做的功Wf=Ffx=40J；
（3）设物块回到底端A时的动能为Ek
由动能定理得：0+0+2(-Wf)=Ek-12mv20，
解得，动能Ek=12mv20+2(-Wf)=20J；
答：（1）物块上滑过程中加速度的大小为10m/s2；
（2）物块上滑过程中克服摩擦力做的功为40J；
（3）物块回到底端A时的动能为20J．

本题解析：

本题难度：一般

3、选择题  质量不计的直角形支架两端分别连接质量为m和2m的小球A和B。支架的两直角边长度分别为2l和l，支架可绕固定轴O在竖直平面内无摩擦转动，如图所示。开始时OA边处于水平位置，由静止释放，则
[? ]

A.B球相对于初始位置上升的最大高度为l
B.A球的速度最大时，两小球的总重力势能为零
C.A球在向下摆的全过程中，杆对它做了负功
D.A、B两球的最大速度之比v1∶v2=2∶1

参考答案：ACD

本题解析：

本题难度：一般

4、计算题  （10分）如图所示，内壁粗糙的半圆形碗固定在水平地面上，碗的半径R=1m。质量为2kg的小球自碗口静止释放，滑到碗底时的速度大小为v=4m/s。? (g=10m/s2) 则：
（1）从碗口到碗底小球重力势能的变化是多少？
（2）从碗口到碗底摩擦力对小球做功是多少？
（3）在碗底处，小球对碗底的压力是多少？

参考答案：（1）重力势能减少20J
（2）
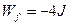
（3）

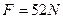
本题解析：（1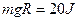）?重力势能减少20J
（2），
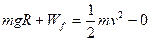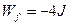
（3），

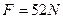
本题难度：简单

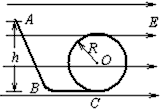
5、计算题  如图所示的装置是在竖直平面内放置光滑的绝缘轨道，处于水平向右的匀强电场中，以带负电荷的小球从高h的A处静止开始下滑，沿轨道ABC运动后进入圆环内作圆周运动。已知小球所受到电场力是其重力的3／4，圆滑半径为R，斜面倾角为θ=53°，sBC=2R。若使小球在圆环内能作完整的圆周运动，h至少为多少？（sin37°=0.6 sin53°=0.8）

参考答案：解：小球所受的重力和电场力都为恒力，故可两力等效为一个力F，如图所示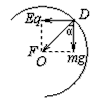可知F＝1.25mg，方向与竖直方向左偏下37°，从图中可知，能否作完整的圆周运动的临界点是能否通过D点，若恰好能通过D点，即达到D点时球与环的弹力恰好为零
由圆周运动知识得：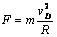
即：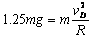
由动能定理有：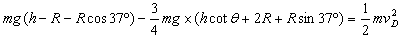
联立①、②可求出此时的高度h=10R

本题解析：

本题难度：困难