1、计算题 如图所示,1、2、3为p-V图中一定质量理想气体的三个状态,该理想气体由状态1经过过程1-3-2到达状态2。试利用气体实验定律证明: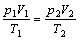 。
。
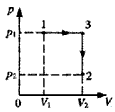
参考答案:解:设状态3的温度为T
1-3为等压过程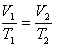
3-2为等容过程
消去T即得
本题解析:
本题难度:一般
2、计算题 如图,一上端开口,下端封闭的细长玻璃管,下部有长l1=66cm的水银柱,中间封有长l2=6.6cm的空气柱,上部有长l3=44cm的水银柱,此时水银面恰好与管口平齐。已知大气压强为P0=76cmHg。如果使玻璃管绕低端在竖直平面内缓慢地转动一周,求在开口向下和转回到原来位置时管中空气柱的长度。封入的气体可视为理想气体,在转动过程中没有发生漏气。

参考答案:解:设玻璃管开口向上时,空气柱压强为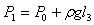 ?①,式中,ρ和g分别表示水银的密度和重力加速度
?①,式中,ρ和g分别表示水银的密度和重力加速度
玻璃管开口响下时,原来上部的水银有一部分会流出,封闭端会有部分真空。设此时开口端剩下的水银柱长度为x,则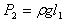 ,
,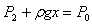 ?②,式中,P2管内空气柱的压强
?②,式中,P2管内空气柱的压强
由玻意耳定律得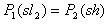 ③,式中,h是此时空气柱的长度,S为玻璃管的横截面积
③,式中,h是此时空气柱的长度,S为玻璃管的横截面积
由①②③式和题给条件得h=12cm ④
从开始转动一周后,设空气柱的压强为P3,则 ⑤
⑤
由玻意耳定律得 ⑥,式中,h"是此时空气柱的长度
⑥,式中,h"是此时空气柱的长度
由①②③⑤⑥h"≈9.2cm ⑦
本题解析:
本题难度:一般
3、选择题
如图所示,一导热性能良好的气缸吊在弹簧下,缸内被活塞封住一定质量的气体(不计活塞与缸壁摩擦),当温度升高到某一数值时,变化了的量有( )
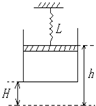
A.活塞高度h
B.缸体高度H
C.气体压强p
D.弹簧长度L
参考答案:B
本题解析:
本题难度:简单
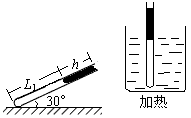
4、计算题 如图所示,长为50cm粗细均匀的细玻璃管的一端开口另一端封闭,在与水平方向成30°角放置时一段长为h=20cm的水银柱封闭着一定质量的理想气体,管内气柱长度为L1=30cm,大气压强P0=76cmHg,室温t1=27℃。现将玻璃管沿逆时针方向缓慢转过60°,使它下端浸入冰水混合物中,足够长的时间后对冰水混合物进行加热。
(1)求管内气柱长度的最小值;
(2)为了保证水银不会从管内溢出,求水温升高的最大值;
(3)如果水温升高到最大值后继续加热,管内气柱长度的变化与水温变化是否满足线性关系?为什么?
参考答案:解:(1)
解得:L2=24.46cm
(2)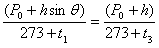
解得:t3=61.88℃
(3)管内气柱长度的变化与水温变化不否满足线性关系,因为不是等压变化
本题解析:
本题难度:一般
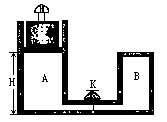
5、简答题 如图所示,气缸的横截面积为S,它与容器B用一个带阀门K的细管连通(细管容积不计).开始时K关闭,气缸A内充有一定质量的理想气体,B内为真空,气缸A的活塞上放有砝码,此时A内气体温度为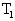 ,活塞静止时与气缸底部的距离为H,打开阀门K后,活塞下降.若将A、B内气体的温度都升高到
,活塞静止时与气缸底部的距离为H,打开阀门K后,活塞下降.若将A、B内气体的温度都升高到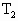 时,活塞仍可升高到原来的高度H.再让A、B内气体的温度恢复到
时,活塞仍可升高到原来的高度H.再让A、B内气体的温度恢复到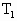 ,并将活塞上的砝码取走,这时活塞又恢复到原来的高度H.若已知大气压强为
,并将活塞上的砝码取走,这时活塞又恢复到原来的高度H.若已知大气压强为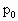 ,活塞质量为m,活塞与气缸间摩擦可忽略不计.求容器B的容积
,活塞质量为m,活塞与气缸间摩擦可忽略不计.求容器B的容积 和活塞上砝码的质量m.
和活塞上砝码的质量m.
参考答案:
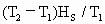 ?,?
?,?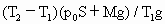
本题解析:
以B中气体为研究对象,
初态(状态1): =HS,
=HS, +(M+m)g/S,
+(M+m)g/S,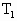 ;
;
状态2: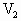 =HS+
=HS+
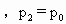 +(M+m)g/S,
+(M+m)g/S,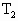 ;
;
状态3: =HS+
=HS+ ,
,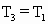
气体由状态1到状态2,初、末压强相等,根据气态方程有
HS/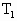 =
=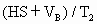 ,
,
解的容器的容积
 =
=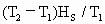 ,
,
气体由状态2到状态3,初、末状态体积相等,根据气态方程有
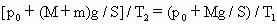 ,
,
解得活塞上砝码的质量
m=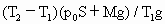 .
.
本题难度:简单