1、简答题  如图所示，粗糙弧形轨道AB和两个光滑半圆轨道组成翘尾巴的S形轨道．光滑半圆轨道半径为R，两个光滑半圆轨道连接处CD之间留有很小空隙，刚好能够使小球通过，CD之间距离可忽略．粗糙弧形轨道最高点A与水平面上B点之间的高度为h从A点静止释放一个可视为质点的小球，小球沿翘尾巴的S形轨道运动后从E点水平飞出，落到水平地面上，落点到与E点在同一竖直线上B点的距离为s．已知小球质量m，不计空气阻力，求：
（1）小球从E点水平飞出时的速度大小；
（2）小球运动到半圆轨道的B点时对轨道的压力大小；
（3）小球沿翘尾巴S形轨道运动时克服摩擦力做的功．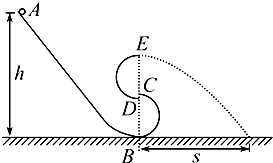

参考答案：（1）（1）小球从E点飞出后做平抛运动，设在E点的速度大小为v，则：
4R=12gt2
s=vt
解得：v=s

本题解析：

本题难度：一般

2、选择题  关于平抛运动，下列说法中正确的是（　　）
A．从同一高度，以不同的速度同时水平抛出两个物体，它们一定同时着地，但抛出的水平距离一定不同
B．从不同高度，以相同的速度同时水平抛出两个物体，它们一定不能同时落地，抛出的水平距离也一定不同
C．从不同高度，以不同速度同时水平抛出两个物体，它们一定不能同时着地，抛出的水平距离也一定不同
D．以上说法都不对

参考答案：A、根据t=

本题解析：

本题难度：一般

3、简答题  如图所示，一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接，一小球以v0=5m/s的速度在水平面上向右运动．求小球从A点运动到地面所需的时间（平面与斜面均光滑．g取10m/s2）．某同学对此题的解法为：小球沿斜面运动，则

参考答案：不同意上述解法，小球应在A点离开平面做平抛运动，而不是沿斜面下滑．正确的解法是：
假如小球直接落至地面，则小球在空中运动的时间为
t=

本题解析：

本题难度：一般

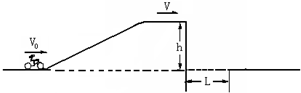
4、简答题  如图所示，摩托车运动员做飞越壕沟的特技表演，摩托车以初速度V0冲上顶部水平的高台，高台后面是一条宽L=10m的壕沟，若摩托车冲上高台过程中以恒定功率P=1.8kW行驶，经历时间t=5s，到达高台顶部时立即关闭发动机，摩托车在水平的高台上做匀速直线运动一段距离后飞离高台．已知人和车的总质量m=180kg（可视为质点），平台高h=5m，忽略空气阻力和摩擦阻力．取g=10m/s2．问：
（1）V0至少应多大？
（2）假定摩托车落地速度大小超过Vm=30m/s时会对运动员造成危险，则摩托车飞离高台时的最大速度Vm′应为多少？

参考答案：（1）设刚好能越过壕沟的水平速度为v1，则：h=12gt12
L=v1t1
联以上两式代入数据得v1=10m/s
由动能定理Pt-mgh=12mv12-12mv02
代入数据解得v0=10m/s
（2）由机械能守恒定律，规定地面为零势能参考平面有12mvm’2+mgh=12mvm2
代入数据解得Vm′=20

本题解析：

本题难度：一般

5、选择题  将一个小球以速度v水平抛出，使小球做平抛运动．要使小球能够垂直打到一个斜面上，斜面与水平方向的夹角为α．那么（　　）
A．若保持水平速度v不变，斜面与水平方向的夹角α越大，小球的飞行时间越长
B．若保持斜面倾角α不变，水平速度v越大，小球飞行的水平距离越长
C．若保持斜面倾角α不变，水平速度v越大，小球飞行的竖直距离越短
D．若只把小球的抛出点竖直升高，小球仍能垂直打到斜面上

参考答案：A、小球垂直碰撞在倾角为α的斜面上，速度与斜面垂直，速度与竖直方向的夹角为α，则有：vyv=1tanα；竖直分速度：vy=gt；则得t=vgtanα
可知若保持水平速度ν不变，α越大，飞行时间越短．故A错误；
B、若保持斜面倾角α不变，由上式知水平速度v越大，则小球的运动时间t变长，故水平分位移x=vt一定变大，故B正确；
C、若保持斜面倾角α不变，水平速度v越大，则小球的竖直飞行的速度也变大，时间变长，故竖直分位移y=12gt2变大，故C错误；
D、若只把小球的抛出点竖直升高，假设斜面足够长，小球轨迹向上平移，仍能垂直打到斜面上，但斜面长度是一定的，故不一定打到斜面上，故D错误；
故选：B

本题解析：

本题难度：简单