1、简答题  如图所示，水平桌面处有水平向右的匀强电场，场强大小E=2×104V/m，A、B是完全相同的两个小物体，质量均为m=0.1kg，电量均为q=2×10-5C，且都带负电，原来都被按在桌面上的P点．现设法使A物体获得和电场E同方向的初速vA0=12m/s，A开始运动的加速度大小为6m/s2，经τ时间后，设法使B物体获得和电场E同方向的初速vB0=6m/s（不计A、B两物体间的库仑力），求：
（1）在A未与B相遇前，A电势能增量的最大值；
（2）如果要使A尽快与B相遇，τ为多大？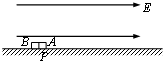

参考答案：（1）A释放后，根据牛顿第二定律有
? qE+f=ma，得f=0.2N，
A速度减到零所用时间为 t=vAOa=2s，
经过的位移为s=v2AO2a=12m，
所以在A未与B相遇前，A电势能增量的最大值为△Emax=qEs=4.8J．
（2）因为B的速度较小，要尽快相遇，对应B减速到零时与A相遇，
B的最大位移为 sB=v2BO2a=3m，花时tB=vBOa=1s，
对于A：返回时qE-f=ma′，得a′=2m/s2．
A返回走了s′=s-sB=9m，用时tA=

本题解析：

本题难度：一般

2、填空题  某物块以80J初动能从固定斜面底端上滑，以斜面底端为零势能参考平面，到达最高点时物块的重力势能为50J．在返回斜面底端的过程中，当物块的重力势能为20J时，动能为______J；当物块下滑到动能和势能恰好相等时，其机械能为______J．

参考答案：从斜面底端到顶部过程，根据动能定理，有：-mgxsinθ-fx=0-80? ①
在最高点，重力势能为：mgxsinθ=50? ②
下滑过程，根据动能定理，有：mgx1sinθ-fx1=Ek-0? ③
此时重力势能为：mg（x-x1）sinθ=20? ④
联立①②③④式，解得：Ek=12J；
当物块下滑到动能和势能恰好相等时，假设下滑位移为x2，对从最高点到该点过程，根据动能定理，有：
mgx2sinθ-fx2=Ek2-0? ⑤
此位置，有：Ek2=Ep2? ? ⑥
Ep2=mg（x-x2）? ⑦
联立①②⑤⑥⑦解得：Ek2=Ep2=1007J，故机械能E=Ek2+Ep2=200J7≈28.6J；
故答案为：12，28.6．

本题解析：

本题难度：一般

3、简答题  如图所示，N匝矩形金属线圈的质量为m，电阻为R，放在倾角为θ的光滑斜面上，其ab边长度为L且与斜面底边平行．与ab平行的两水平虚线MN、PQ之间，在t=0时刻加一变化的磁场，磁感应强度B大小随时间t的变化关系为B=Kt，方向垂直斜面向上．在t=0时刻将线圈由图中位置静止释放，在t=t1时刻ab边进入磁场，t=t2时刻ab边穿出磁场．线圈ab边刚进入磁场瞬间电流为0，穿出磁场前的瞬间线圈加速度为0．（重力加速度为g）求：

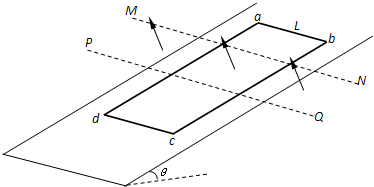
（1）MN、PQ之间的距离d；
（2）从t=0到t=t1运动过程中线圈产生的热量Q；
（3）线圈的ab边在穿过磁场过程中克服安培力所做的功W．

参考答案：（1）线圈进入磁场前做匀加速运动，
由牛顿第二定律得：mgsinθ=ma，a=gsinθ，
当t=t1时，线圈的速度：v1=at1=gsinθt1…①
由法拉第电磁感应定律得，由于磁场变化产生的感应电动势：
E1=N△Φ△t=NS△B△t=NdlKt1-0t1-0=NKld，
ab边切割磁感线产生的感应电动势：
E1′=NB1lv1=NKlgt12sinθ，
由题意可知瞬间电流为0，
则：E合=E1-E1′=0
即：NKdl=NKlgt12sinθ，
∴磁场宽度：d=gt12sinθ；
（2）由（1）可知：E1=NKld，感应电流：I=E1R=NKldR，
从t=0到t=t1运动过程中线圈产生的热量Q：
?Q=I2Rt1=N2k2L2g2sin2θt51R；
（3）当t=t2时，由题意知：mgsinθ-NB2I2L=0，
设ab边穿出磁场瞬间的速度为v2，
ε2=NB2Lv2，I2=NB2Lv2R，
∴v2=mgRsinθN2k2t2L2，
由动能定理：12mv22-12mv21=mgdsinθ-W，
解得：W=12mg2sin2θ(3t21-m2R2N4k4t42L4)；
答：（1）MN、PQ之间的距离为gt12sinθ；
（2）从t=0到t=t1运动过程中线圈产生的热量为N2K2L2g2(sinθ)2t51R；
（3）线圈的ab边在穿过磁场过程中克服安培力所做的功为12mg2sin2θ(3t21-m2R2N4K4L4t42)．

本题解析：

本题难度：一般

4、选择题  如图所示，拉力F将物体沿斜面拉下，已知拉力大小与摩擦力大小相等，则下列说法中正确的是（　　）
A．物体的总机械能增加
B．物体的总机械能保持不变
C．物体的总机械能减少
D．合外力对物体做功为零