1、计算题  如图所示，真空中相距d="5" cm的两块平行金属板A、B与电源连接（图中未画出），其中B板接地（电势为零），A板电势变化的规律如图所示.
将一个质量m=2.0×10-23 kg，电量q=+1.6×10-15C的带电粒子从紧临B板处释放，不计重力.求：

（1）在t=0时刻释放该带电粒子，释放瞬间粒子加速度的大小;
（2）若在t=时刻从紧临B板处无初速释放该带电粒子，粒子恰好不能到达A板，试求 A板电势变化的周期为多大？

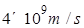参考答案：（1）（2）

本题解析：
电场强度：，且　解得：
（2）带电粒子在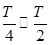向A板做匀加速运动，在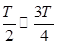向A板做匀减速运动，速度减为零后将返回，粒子向A板运动可能的最大位移：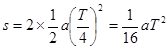　
要求粒子恰好不能到达A板，有，s=d

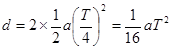
解得：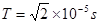 
考点：带电粒子在电场中的运动。

本题难度：一般

2、选择题  带电粒子（不计重力）以初速度V0从a点进入匀强磁场，如图8。运动中经过b点，oa=ob。若撤去磁场加一个与y轴平行的匀强电场，仍以V0从a点进入电场，粒子仍能通过b点，那么电场强度E与磁感强度B之比E/B为：（?）

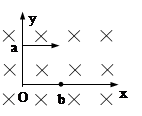
A．V0
B．1
C．2V0
D．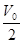

参考答案：C

本题解析：带电粒子在磁场中做匀速圆周运动，则由洛仑兹力提供向心力可知

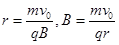
加上电场后，粒子进入电场做的是类平抛运动，由水平和竖直分运动特点，有
，C对；
点评：本题难度中等，关键是弄清楚粒子在电场和磁场中的运动性质，找到两个运动的相同点，代入公式推导

本题难度：一般

3、计算题  (12分)在如图所示的直角坐标系xoy中，矩形区域oabc内有垂直于纸面向外的匀强磁场，磁感应强度大小为B=5.0×10-2T；第一象限内有沿-y方向的匀强电场，电场强度大小为E=1.0×105N／C．已知矩形区域oa边长为0．60m，ab边长为0.20 m．在bc边中点N处有一放射源，某时刻，放射源沿纸面向磁场中各方向均匀地辐射出速率均为m/s的某种带正电粒子，带电粒子质量m=1.6×10-27kg，电荷量为q=+3.2×10-19kg，不计粒子重力，求：(计算结果保留两位有效数字)

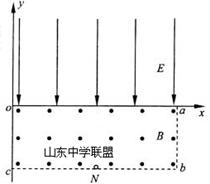
(1)粒子在磁场中运动的半径；
(2)从x轴上射出的粒子中，在磁场中运动的最短路程为多少?
(3)放射源沿-x方向射出的粒子，从射出到从y轴离开所用的时间．

参考答案：⑴ 0.20m  ⑵ 0.21m ⑶ 4.6×10-7s

本题解析：⑴轨迹如图，由牛顿第二定律得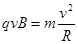（1分）

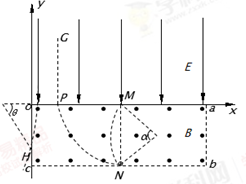
解得R=0.20m   （1分）
⑵由数学知识可知最短的弦对应最短的弧长
由图可知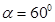：（1分）
最短的弧长即最短的路程   （1分）
⑶粒子在磁场中的周期          （1分）
粒子在磁场中沿NP运动的时间          （1分）
粒子在电场中的加速度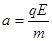       （1分）
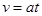又       （1分）
解得粒子在电场中往返运动的时间为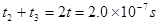     （1分）
由图可知
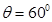       （1分）
粒子在磁场中运动的第二部分时间 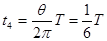        （1分）
粒子运动的总时间 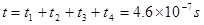        （1分）
考点：带电粒子在匀强磁场中的运动、带电粒子在电场中的运动

本题难度：困难

4、计算题  （22分）如图所示，电子显像管由电子枪、加速电场、偏转磁场及荧光屏组成。在加速电场右侧有相距为d、长为l的两平板，两平板构成的矩形区域内存在方向垂直纸面向外的匀强磁场，磁场的右边界与荧光屏之间的距离也为d。荧光屏中点O与加速电极上两小孔S1、S2位于两板的中线上。从电子枪发射质量为m、电荷量为

参考答案：

本题解析：

本题难度：一般

5、选择题  空间存在一电场，一带负电的粒子仅在电场力作用下从x1处沿x轴负方向运动，初速度大小为v0,其电势能Ep随坐标x变化的关系如图所示，图线关于纵轴左右对称，以无穷远处为零电势能点，粒子在原点O处电势能为E0，在x1处电势能为E1，则下列说法中不正确的是（?）

A．坐标原点O处电场强度为零
B．粒子经过x1、-x1处速度相同
C．由x1运动到O过程加速度一直减小
D．粒子能够一直沿x轴负方向运动，一定有

参考答案：C

本题解析：从图中可得负电粒子的电势能先增大，后减小，说明电场力先做负功后做正功，O点是分界点，在O点电场方向发生变化，所以O点的电场强度为零，A正确；在x1、-x1处电势能大小相等，所以整个过程中电场做功之和为零，故动能不变，即两处的速度相等，B正确；电场力的功等于电势能的减少量，故图像斜率为电场力的大小，从图中可得从x1到O点运动过程中，电场力先增大后减小，加速度先增大后减小，C错误；要使粒子一直沿x负方向运动，从图中可得则初速度必须满足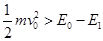,故，D正确，故选C。

本题难度：一般