1、计算题   (18分)如图所示，ABCD是边长为L的正方形，在其中的适当区域内有匀强磁场，磁场方向垂直纸面向里。质量为m、电荷量为q的粒子以大小为v的速度垂直BC边从C点射入正方形区域，所经过的区域都有磁场，最后从A点射出磁场。不计粒子重力。求：
（1）匀强磁场的磁感应强度B的大小？
（2）若完全相同的粒子以相同的速度从BC的中点O垂直BC边射入正方形区域，在到达P点前，所经过的区域没有磁场，从P点开始，所经过的区域都有磁场，最后从A点射出磁场。则P点到BC边的距离x＝?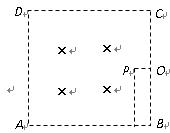

参考答案：（1）B＝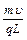
（2）x＝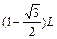

本题解析：（1）粒子垂直BC边从C点射入正方形区域，最后从A点射出磁场，圆弧CEA是运动轨迹，由于圆心一定在CB或CB的延长线上，也一定在A、C连线的中垂线上，所以B点是圆心，设圆弧的半径为r，粒子受到的洛伦兹力为 f，则
r＝L?………………（2分）
f＝qvB?………………（2分）
根据牛顿第二定律f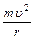＝?………………（2分）
解得B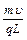＝?………………（2分）
（2）粒子从BC的中点O垂直BC边射入正方形区域，从P点开始，做匀速圆周运动，最后从A点射出磁场，圆弧PFA是运动轨迹，半径仍然为r，设圆心为O1，在△APO1中，有

PO1＝r?………………（1分）
AO1＝r?………………（1分）
由于PP1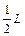＝?………………（1分）
所以P1O1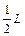＝，即AP1是PO1的中垂线，所以
AP＝AO1＝L?………………（2分）
AP1＝AB－P1B＝L－x?…………（1分）
在△APP1中，有
(AP)2＝(AP1)2＋(PP1)2?…………（2分）
即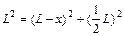
解得x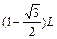＝?…………（2分）

本题难度：简单

2、选择题  如图，在竖直平面内放一个光滑绝缘的半圆形轨道，水平方向的匀强磁场与半圆形轨道所在的平面垂直。一个带正电荷的小滑块由静止开始从半圆轨道的最高点M滑下，则下列说法中正确的是（?）

A．滑块经过最低点时的速度与磁场不存在时相等
B．滑块从M点滑到最低点所用的时间与磁场不存在时相等
C．滑块从左往右与从右往左经过最低点时，所受洛伦兹力相同
D．滑块从左往右与从右往左经过最低点时，向心加速度相同

参考答案：ABD

本题解析：略

本题难度：简单

3、计算题   (选修3－1的考生做) (8分)
如图所示，一个电子的质量为m，电荷量为e，让它以初速度v0，从屏S上的O点垂直于S射入其右边区域。该区域有垂直于纸面向里、磁感应强度为B的匀强磁场，该区域为真空。
(1)求电子回到屏S时距离O点有多远；
(2)若电子在磁场中经过某点P，OP连线与v0成θ=600角，求该电子从O点运动到P点所经历的时间t。

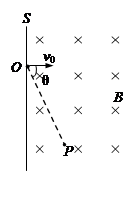
参考答案：（1）电子进入磁场后在洛伦兹力作用下做匀速圆周运动，，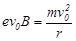
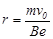
当它回到S屏时，刚好运动半周，其距离O点的距离为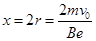?（4分）
（2）由几何知识电子到达P点时所对应的圆心角α=1200
所用时间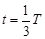
由?
故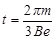?（4分）

本题解析：略

本题难度：简单

4、简答题  在一个水平放置的、半径为r的圆形管道内存在着匀强磁场，磁感强度大小为B，方向如图所示．管道轴线左端为Ｏ点，右端为Ｏ’点，OO’＝l．一个质量为m、带电量为＋q的质点沿管道轴线从左边射入，经过Ｏ点时速度大小为v０，方向指向Ｏ’点．要使质点在运动过程中能经过Ｏ’点，讨论速度v０的可能取值．

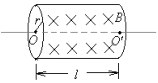
参考答案：若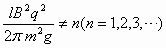，则v0只能取唯一值，即
若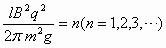，则v0可取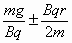之间的任意值．

本题解析：
如果质点进入磁场后受力平衡，则质点做匀速直线运动，此时速度为v01，
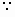mg=Bqv01，．
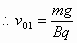若质点初速v0≠v01，则可以把v0分解为同一直线上的两个速度，即
v0=v01+v0’(v0’可正可负)
质点的运动可以看作两个运动的合运动，一个是以v01作匀速直线运动，另一个是速率为v0’的匀速圆周运动．半径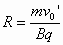周期．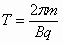
要能通过O’点，必须满足nT=l/v01(n=1,2,3…)
又，为了不使质点运动时与管壁相碰，应满足r>2R，即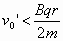
结论：若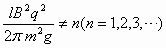，则v0只能取唯一值，即
若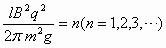，则v0可取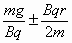之间的任意值．

本题难度：简单

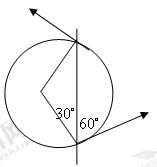
5、选择题  如图所示，在第Ⅰ象限内有垂直纸面向里的匀强磁场，一对正、负电子分别以相同速率沿与X轴成300角的方向从原点射入磁场，则正、负电子在磁场中运动的时间之比为(? )

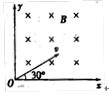
A．1:2
B．2:1
C．
D．1:1

参考答案：B

本题解析：正、负电子分别以相同速率沿与X轴成300角的方向从原点射入磁场,速度与磁场垂直，洛伦兹力提供向心力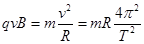，速度相同，电荷量相同，所以半径相同周期相同。正电子偏向纵轴，在水平边界的匀强磁场中运动轨迹如下图左图，转过的圆心角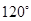为运动时间为，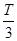
负电子偏向横轴，在水平边界的匀强磁场中运动轨迹如下图，转过的圆心角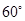为运动时间为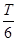，所以正负电子运动时间之比为2:1，选项B对。

本题难度：一般