1、选择题 一匀强磁场,磁场方向垂直于xOy平面,在xOy平面上,磁场分布在以O为圆心的一个圆形区域内。一个质量为m、电荷量为q的带电粒子,由原点O开始运动,初速度为v,方向沿x轴正方向。后来,粒子经过y轴上的P点,如图所示。不计重力的影响。粒子经过P点时的速度方向可能是图中箭头表示的 ?(?)

A.只有箭头a、b是可能的
B.只有箭头b、c是可能的
C.只有箭头c是可能的
D.箭头a、b、c、d都是可能的
参考答案:B
本题解析:
分析:一带电粒子,以一定的速度垂直进入匀强磁场中,由洛伦兹力提供向心力,使其做匀速圆周运动.若P点在磁场中,则由粒子运动轨迹来确定经过P点的速度方向;若P点不在磁场中,则粒子先做匀速圆周运动后,做直线运动,从而确定粒子经过P点的速度方向.
解答:解:磁场分布在以O为圆心的一个圆形区域内,由于半径不知,所以当P点在磁场中,则粒子从O点沿x轴正方向,当到达P点时,刚好完成半圈.所以经过P点的速度方向指向C;
当磁场分布在以O为圆心的一个圆形区域内,由于半径不知,所以当P点在磁场之外,则粒子从O点沿x轴正方向,因此出磁场时,还没有到达P点,接着做匀速直线运动后到达P点时,所以经过P点的速度方向指向b;
因此速度方向不可能指向a 或d.
故选:B
本题难度:一般
2、选择题 如题图所式,矩形MNPQ区域内有方向垂直于纸面的匀强磁场,有5个带点粒子从图中箭头所示位置垂直于磁场边界进入磁场,在纸面内做匀速圆周运动,运动轨迹为相应的圆弧,,这些粒子的质量,电荷量以及速度大小如下表所示。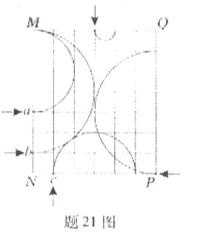
粒子编号
| 质量
| 电荷量(q>0)
| 速度大小
|
1
| m
| 2q
| v
|
2
| 2m
| -2q
| 2v
|
3
| 3m
| -3q
| 3v
|
4
| 2m
| 2q
| 3v
|
5
| 2m
| -q
| v
|
?
由以上信息可知,从图中abc处进入的粒子对应表中的编号分别为
A.3,5,4? B.4,2,5
C.5,3,2? D.2,4,5
参考答案:D
本题解析:由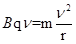 ?可知,半径公式
?可知,半径公式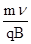 ?;
?;
结合表格中数据可求得1-5各组粒子的半径之比依次为0.5:2:3:3:2,说明第一组正粒子的半径最小,由图可知故该粒子从MQ边界进入磁场逆时针运动.
由图a、b粒子进入磁场也是逆时针运动,则都为正电荷,而且a、b粒子的半径比为2:3,则a一定是第2组粒子,b是第4组粒子.c顺时针运动,都为负电荷,半径与a相等是第5组粒子.
本题看似比较复杂,但只要认真分析即可发现半径大小以及偏转方向的关系,则根据带电粒子圆周运动的性质可得出正确结果.
本题难度:一般
3、选择题 在物理学史上,首先提出磁场对运动电荷有力的作用的科学家是
[? ]
A.欧姆
B.安培
C.洛伦兹
D.法拉第
参考答案:C
本题解析:
本题难度:简单
4、计算题 如图所示,有两个磁感应强度均为B、但方向相反的匀强磁场,OP是它们的分界面。有一束电量均为q、但质量不全相同的带电粒子,经过相同的电场加速后,从O处沿与OP和磁场都垂直的方向进入磁场,在这束粒子中有一些粒子的轨迹如图所示。已知OP=L,加速电场的电势差为U,重力不计,问。
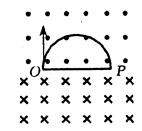
(1)按图示的轨迹到达P点的每个粒子的质量m为多大?
(2)在这束粒子中,质量为m的多少倍的粒子也可能到达P点?(设质量为m1)
参考答案:(1)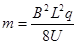 (2)
(2)
本题解析:粒子在电场中加速? qU=
在磁场中轨道半径? r=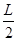
洛伦兹力提供向心力? qvB=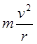
解得 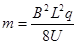
(2)设质量m1.粒子在电场中加速? qU=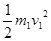
在磁场中轨道半径? L=n.2r1? (n=2.3.4…….)
洛伦兹力提供向心力? qv1B=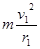
解得?
则质量为原质量的 倍? (n=2.3.4……..)
倍? (n=2.3.4……..)
点评:在垂直的磁场中做匀速圆周运动.圆周运动的可建立几何关系来列式求解.
本题难度:一般
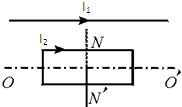
5、选择题 如图所示,一根通有电流I1的固定长直导线在通有电流I2的矩形线圈的平面内,线圈将会出现( )
A.远离导线运动
B.向着导线平动
C.绕轴OO′运动
D.绕轴NN′运动