1、简答题  如图，水平地面上有一个坑，其竖直截面为半圆．ab为沿水平方向的直径．若在a点以初速度v0沿ab方向抛出一小球，小球会击中坑壁上的c点．已知c点与水平地面的距离为圆半径的一半，求圆的半径．

参考答案：设圆半径为r，质点做平抛运动，设水平方向的位移为x，竖直方向上的位移为y，
则：x=v0t--------------①
y=0.5r=12gt2---------②
过c点做cd⊥ab于d点，Rt△acd∽Rt△cbd可得


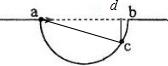
cd2=ad?db
即为：(r2)2=x(2r-x)--------③
由①②③得：r=4(7±4

本题解析：

本题难度：一般

2、填空题  在“研究平抛运动”的实验中，可以描绘物体平抛运动的轨迹和求出物体平抛运动的初速度。现已测出物体平抛运动曲线上某点的坐标为x 、y ，用表达式v0 =           可以求出该小球的平抛运动的初速度。

参考答案：

本题解析：由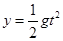可得飞行时间，初速度。
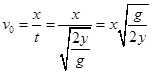考点：平抛运动
点评：平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动，根据竖直位移求时间，根据水平位移求初速度。

本题难度：一般

3、填空题  以速度v0水平抛出一小球，忽略空气阻力，当小球的水平位移与竖直位移大小相等时，小球速度的大小为___________m/s，小球在空中运动的时间是______s。

参考答案：，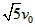

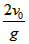
本题解析：

本题难度：一般

4、简答题  如图所示，从光滑的

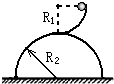
参考答案：（1）小球滑出槽口时速度为v，
根据机械能守恒定律得：mgR1=12mv2①
在槽口时：N-mg=mv2R1②
由①②式解得：N=3mg
由牛顿第三定律得：N′=N=3mg?方向：竖直向下
（2）若要使小球滑出槽口后不沿半球面下滑，可知重力恰好或不足以提供向心力而作平抛运动．
即mg≤mv2R2③
由①③两式联立解得R1与R2应满足的关系是：
R1≥12R2
（3）由机械能守恒得：Ek=12mv2+mgR2=32mgR2
答：（1）小球运动到14圆弧槽的底部对圆弧槽的底部压力为3mg，方向竖直向下；
（2）若要使小球滑出槽口后不沿半球面下滑，则R1与R2应满足R1≥12R2；
（3）若小球刚好不沿半球面下滑，则小球落地时的动能为32mgR2．

本题解析：

本题难度：一般

5、计算题  小球以15 m/s的水平初速度向一倾角为37°的斜面抛出，飞行一段时间后，恰好垂直撞在斜面上。求：

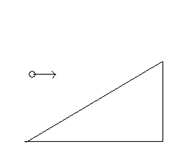
（1）小球在空中的飞行时间；
（2）抛出点距落球点的高度。（sin370="0.6?" cos370=0.8）

参考答案：解：将球垂直撞在斜面上的速度分解，如图6-4-7所示.由图可知

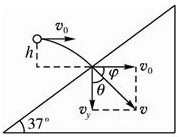
θ=37°,φ=90°-37°=53°……2分
tanφ=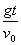，则t=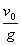·tanφ= 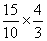s="2" s……4分
h=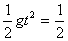×10×22 m="20" m.……4分

本题解析：略

本题难度：简单