1、选择题  在图所示的直角坐标系xyz所在的区域内，存在电场强度为E的匀强电场和磁感强度为B的匀强磁场。已知从坐标原点O沿x轴的正方向射入质子，穿过这区域时未发生偏转。设重力可忽略不计，则这区域中的E和B的方向可能是 （?）

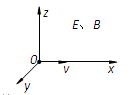
A．E和B都沿x轴的正方向
B．E和B都沿x轴的负方向
C．E沿z轴正方向，B沿y轴正方向
D．E沿z轴正方向，B沿y轴负方向

参考答案：ABC

本题解析：带电粒子在混合场中的运动．
分析：根据各选项提供的电场方向和磁场方向，逐一分析各选项中的受力情况，分析电场力和磁场力的合力，即可判断带电粒子的运动情况．
解：A、B选项中，磁场对粒子作用力为零，电场力与粒子运动方向在同一直线，方向不会发生偏移，A、B正确．
C选项中，电场力沿z轴正方向、洛伦兹力都是沿z轴负方向，二力平衡，将做直线运动，C错误．
D选项，电场力沿z轴正方向，洛伦兹力沿z轴正方向，两力同向，二力不会平衡，粒子将做曲线运动，D错误．故选ABC．

本题难度：简单

2、选择题  如图所示，一束粒子（不计重力，初速度可忽略）缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I，再通过小孔O2射入相互正交的匀强电场和匀强磁场区域II，其中磁场的方向如图所示，磁感应强度大小可根据实际要求调节，收集室的小孔O3与O1、O2在同一条水平线上.则

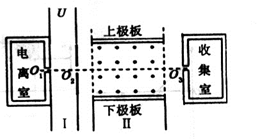
A．该装置可筛选出具有特定质量的粒子
B．该装置可筛选出具有特定电荷量的粒子
C．该装置可筛选出具有特定比荷的粒子
D．该装置可筛选出具有特定功能的粒子

参考答案：C

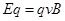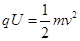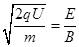本题解析：在复合场中，粒子所受电场力与洛伦兹力合力为0，即，可得，该装置筛选出的是具有特定比荷的粒子，C对。

本题难度：简单

3、计算题  （10分）如图所示，以AB为界的两匀强磁场，磁感应强度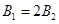，方向垂直纸面向里。现有一质量为m、带电量为q的带正电粒子，从O点沿图示方向进入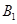中。
（1）试画出粒子的运动轨迹
（2）求经过多长时间粒子重新回到O点？

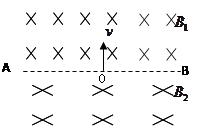
参考答案：（1）见解析（2）()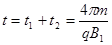

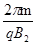本题解析：（1）

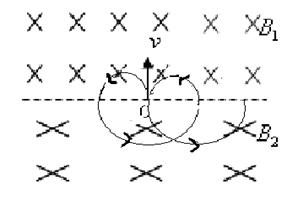
（2）在B1中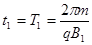：? (2分)?
在B2中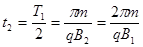：? (2分)?
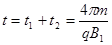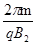()?(1分)

本题难度：一般

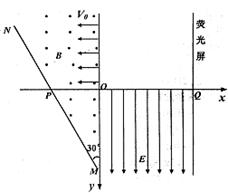
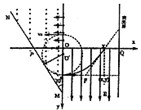
4、计算题  （22分）如图所示，在xOy平面直角坐标系中，直线MN与y轴成30o角，P点的坐标为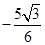（，0），在y轴与直线MN之间的区域内，存在垂直于xOy平面向外、磁感应强度为B的匀强磁场。在直角坐标系xOy的第Ⅳ象限区域内存在沿y轴，正方向、大小为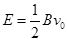的匀强电场，在x=3a处垂直于x轴放置一平面荧光屏，与x轴交点为Q，电子束以相同的速度v0从y轴上0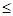y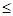2a的区间垂直于y轴和磁场方向射入磁场。已知从y=2a点射入的电子在磁场中轨迹恰好经过O点，忽略电子间的相互作用，不计电子的重力。求：
（1）电子的比荷；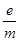
（2）电子离开磁场垂直y轴进入电场的位置的范围；
（3）从y轴哪个位置进入电场的电子打到荧光屏上距Q点的距离最远？最远距离为多少？

参考答案：（1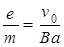）（2）0≤y≤1.5a（3）y=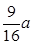时，H有最大值，Hmax=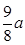

本题解析：（1）由题意可知电子在磁场中的半径为a，由Bev0=m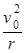
得：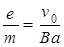
（2）粒子能进入磁场中，且离O点下方最远，则粒子在磁场中运动圆轨迹必须与直线MN相切，粒子轨道的圆心为O′点，

则O′M=2a，由三角函数关系可得：tan30°=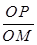
得：OM=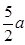
有OO′=0.5a，即粒子在离开磁场离O点下方最远距离为ym=1.5a，从y轴进入电场位置在0≤y≤1.5a范围内．
（3）电子在电场中做类平抛运动，设电子在电场的运动时间为t，竖直方向位移为y，水平位移为x，x=v0t
竖直方向有：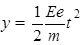
代入得：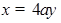
设电子最终打在光屏的最远点距Q点为H，电子射出电场时的夹角为θ，则有：
tanθ=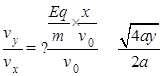
有：H=（3a-x）tanθ=（3a-）?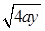
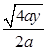
当（3a-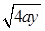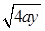）=时，即y=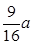时，H有最大值，由于
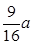＜1.5a，所以Hmax=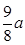

本题难度：一般

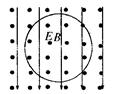
5、选择题  如图所示，匀强磁场的磁感应强度为B，方向垂直于纸面向外，匀强电场场强为E，方向竖直向下，一带电微粒在竖直平面内做匀速圆周运动，不计空气阻力，则?

A．此微粒带正电荷
B．此微粒带负电荷
C．此微粒沿顺时针方向转动
D．此微粒沿逆时针方向转动

参考答案：BD

本题解析：由题意带电微粒在竖直平面内做匀速圆周运动，可知在竖直方向上合外力为零，所以带电粒子的重力和电场力二力平衡，因为电场方向向下，电场力方向向上，所以微粒带负电，B正确；粒子在洛伦兹力的作用下做圆周运动，由左手定则可知微粒沿逆时针方向转动，D正确。

本题难度：一般