1、计算题 某人在距离地面2.6m的高处,将质量为0.2kg的小球以速度v0=12m/s斜向上抛出,小球的初速度方向与水平方向之间的夹角为30°,g取10m/s2,求
(1)人抛球时对球做多少功?
(2)若不计空气阻力,小球落地时的速度大小是多少?
(3)若小球落地时的速度大小为v1=13m/s,小球在空中运动过程中克服阻力做了多少功?
参考答案:解:(1)由动能定理,得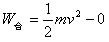 =14.4J
=14.4J
(2)由动能定理,得
所以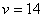 m/s
m/s
(3)由动能定理,得
所以 f=2.7J
f=2.7J
所以克服阻力做功2.7J
本题解析:
本题难度:一般
2、选择题 如图所示,电梯总质量为M,它的水平地板上放置一质量为m的物体,电梯在钢索的拉力作用下由静止开始竖直向上加速运动,当上升高度为h时,电梯的速度达到v,则在这段过程中,以下说法正确的是
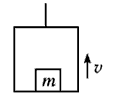
[? ]
A.电梯地板对物体的支持力所做的功等于mv2/2
B.电梯地板对物体的支持力所做的功等于mv2/2+ mgh
C.钢索的拉力做的功等于Mv2/2+ Mgh
D.钢索的拉力做的功大于Mv2/2+ Mgh
参考答案:BD
本题解析:
本题难度:一般
3、计算题 一个质量为m的物体,从倾角为θ,高为h的斜面上端A点,由静止开始下滑,到B点时的速度为v,然后又在水平面上滑行s位移后停止在C点,求:
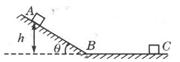
(1)物体从A点开始下滑到B点的过程中克服摩擦力所做的功;
(2)物体与水平面间的动摩擦因数为多大?
参考答案: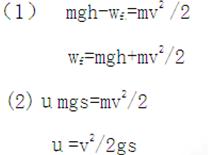
本题解析:略
本题难度:简单
4、简答题 质量为1kg的小球,在空中沿竖直方向加速下落,加速度大小为8m/s2,先后通过空中相距0.75m的A点和B点,若小球在B点的动能是8J.求:
(1)小球在通过AB的过程中动能增加量.
(2)小球在通过A点的速度大小.
参考答案:(1)由牛顿第二定律可得:F=ma=1kg×8m/s2=8N,
由动能定理可得,动能的变化量△EK=Fs=8N×0.75m=6J;
(2)由动能定理得:△EK=EKB-12mvA2,
即:6=8-12×1×vA2,解得:vA=2m/s;
答:(1)小球在通过AB的过程中动能增加量是6J.
(2)小球在通过A点的速度大小为2m/s.
本题解析:
本题难度:一般
5、选择题 人骑自行车下坡,坡长L=500m,坡高h=8m,人和车的总质量为100kg,下坡时初速度为4m/s,人不踏车的情况下,到达坡底时的车速为10m/s,g=10m/s2,则下坡过程中阻力所做的功为(?)
A.-4000J
B.-5000J
C.-3800J
D.-4200J
参考答案:C
本题解析:下坡过程中,重力做正功,阻力做负功,所以根据动能定理可得: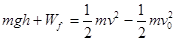 ,代入数据可得
,代入数据可得 ,故C正确,ABD错误,
,故C正确,ABD错误,
点评:在应用动能定理解决问题时,可以不考虑过程,只需要注意始末状态即可,所以动能定理是解决变力做功,多过程问题的首选方法
本题难度:一般