1、简答题  质量为m=5kg的木块，在F=10N的水平恒力作用下，在光滑的水平面上从静止开始运动，运动时间t=5s，求：
（1）木块在t=5s内的位移；
（2）力F在t=5s内对木块做功的平均功率；
（3）5s末木块的动能．

参考答案：（1）根据牛顿第二定律F=ma?
得?a=Fm=105=2（m/s2）?
s=12at2=12×2×25=25（m）
（2）拉力的平均功率.P=Wt=Fst=10×255=50（W）
（3）5s末木块的速度v=at=2×5=10（m/s）
动能Ek=12mv2=12×5×102=250（J）?
答：（1）木块在t=5s内的位移为25m；
（2）力F在t=5s内对木块做功的平均功率为50W；
（3）5s末木块的动能为250J．

本题解析：

本题难度：一般

2、简答题  如图所示，质量为m的小球放在水平地面上，当小球受到与地面成60°的拉力F作用后，小球沿与地面30°方向（虚线所示）做匀加速直线运动．经过t秒后，改变F的大小和方向，使F的沿逆时针方向转过60°．小球沿原方向做匀减速直线运动．求：
（1）开始时F的大小
（2）t秒时小球的速度
（3）小球离地面的最大高度．

参考答案：

（1）小球沿与地面30°方向（虚线所示）做匀加速直线运动，则合力沿与地面30°方向，
做力的合成图，由图可知，mg=F合，
F=2mg?cos30°=

本题解析：

本题难度：一般

3、填空题  某物体的初速度为2m/s，在4 s的时间内速度均匀增大到6m/s，那么该物体的加速度是________ m/s2 ，在这段时间内发生的位移x为      m．

参考答案：1    16

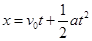本题解析：根据可知，加速度为1m/s2。根据可知，4s内通过的位移为。
考点：匀变速直线运动规律
点评：本题考查了匀变速直线运动规律的推论。通过匀变速公式，比较容易得到结果。

本题难度：一般

4、简答题  如图，质量M=1kg的木板静止在水平面上，质量m=1kg、大小可以忽略的铁块静止在木板的右端．设最大摩擦力等于滑动摩擦力，已知木板与地面间的动摩擦因数μ1=0.1，铁块与木板之间的动摩擦因数μ2=0.4，取g=10m/s2．现给铁块施加一个水平向左的力F．

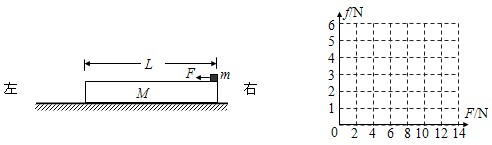
（1）若力F恒为8N，经1s铁块运动到木板的左端．求：木板的长度
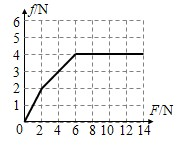
（2）若力F从零开始逐渐增加，且木板足够长．试通过分析与计算，在图中作出铁块受到的摩擦力f随力F大小变化的图象．

参考答案：

（1）由牛顿第二定律：
? 对铁块：F-μ2mg=ma1…①
? 对木板：μ2mg-μ1（M+m）g=Ma2…②
设木板的长度为L，经时间t铁块运动到木板的左端，则
? s木=12a2t2…③
? s铁=12a1t2…④
又：s铁-s木=L…⑤
联立①②③④⑤解得：L=1m…⑥
（2）（i）当F≤μ1（m+M）g=2N时，系统没有被拉动，静摩擦力与外力平衡，即有：f=F
（ii）当F＞μ1（m+M）g=2N时，如果M、m相对静止，铁块与木板有相同的加速度a，则：
? F-μ1（m+M）g=（m+M）a…⑦
? F-f=ma…⑧
解得：F=2f-2…⑨
此时：f≤μ1mg=4N，也即F≤6N…⑩
所以：当2N＜F≤6N时，f=F2+1(N)
（i ii）当F＞6N时，M、m相对滑动，此时铁块受到的摩擦力为：
f=μ2mg=4N
f-F图象如图所示
答：
（1）木板的长度为1m．
（2）f-F图象如图所示．

本题解析：

本题难度：一般

5、计算题  （14分）如图所示，在倾角θ=37°的固定斜面上放置一质量M=1kg、长度L=3m的薄平板AB．平板的上表面光滑，其下端B与斜面底端C的距离为16m．在平板的上端A处放一质量m=0.6kg的滑块，开始时使平板和滑块都静止，之后将它们无初速释放．设平板与斜面间、滑块与斜面间的动摩擦因数均为m=0.5，求滑块与平板下端B到达斜面底端C的时间差Δt．（sin370=0.6，cos370=0.8，g=10m/s2）

参考答案：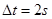

本题解析：对薄板，沿斜面方向由于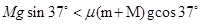，故滑块在薄板上滑动时，薄板静止不动．
对滑块：在薄板上滑行时加速度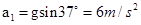，?（2分）
到达B点时速度 ?（2分）
滑块由B至C时的加速度?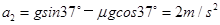?（2分）
设滑块由B至C所用时间为，
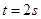则，解得?（2分）
对薄板，滑块滑离后才开始运动，加速度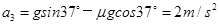， （2分）
滑至C端所用时间为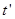，则，解得?（2分）
滑块与平板下端B到达斜面底端C的时间差为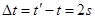：?（2分）

本题难度：一般