1、选择题  在光滑水平面上有一质量为2Kg的物体，受几个共点力作用做匀速直线运动，现突然将与速度反方向的2N的作用力水平旋转600，，则关于 物体运动情况的叙述正确的是? (? )
A．物体做速度大小不变的曲线运动
B．物体做加速度为1m/s2的匀变速曲线运动
C．物体做非匀变速曲线运动，其速度越来越大
D．物体做速度越来越大的曲线运动

参考答案：BD

本题解析：共点力作用下物体平衡专题．物体原来做匀速直线运动，2N的力与其余力的合力大小相等，方向相反．将与速度反方向的2N的作用力水平旋转60°时，该力与其余力的合力夹角为120°，这时物体的合力大小为2N，方向与速度的夹角为60°，合力将做正功，速度增大．根据物体的受力情况分析物体的运动情况．
将与速度反方向的2N的作用力水平旋转60°时，该力与其余力的合力夹角为120°，这时物体的合力大小为2N，方向与速度的夹角为60°，物体做曲线运动．合力将做正功，速度增大．根据牛顿第二定律得加速度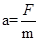=1m/s2，则物体做加速度为1m/s2的匀变速曲线运动．

本题难度：简单

2、计算题  梭梭板（滑板）是儿童喜欢的游乐项目，如图所示，滑板的竖直高度AB为3m，斜面长AC为5m，斜面与水平部分由一小段圆弧平滑的连接。一个质量m为20kg的小孩从滑板顶端由静止开始滑下，最后滑到水平部分上的E点静止。已知小孩与滑板之间的动摩擦因素μ为0.5，不计空气阻力，g取10m/s2，求：

（1）小孩滑到滑板底端C时的速度多大；
（2）小孩从A点开始滑到E点的时间。

参考答案：（1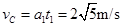）（2）

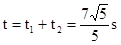
本题解析：小孩在AC上做初速度为0的匀加速运动，设加速度为a1，由牛顿定律知
???

?
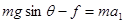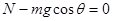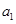
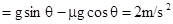设小孩从A到C时间为t1，到C点速度为vC，有
?
?
?
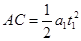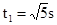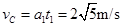在CD上，设加速度为a2，E点速度为0，有
??
?
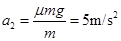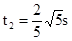故所求时间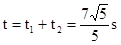

本题难度：一般

3、计算题  如图所示，一辆质量为M=2 kg、长L=2. 25 m的小车放在光滑水平面上。小车的左端上表面与四分之一光滑网弧轨道PQ的底端Q相切，圆弧轨道的半径为R= 1.8 m、固定在竖直平面内。小车的上表面离地面高度为h=0.8 m。一质量为m=1 kg 的小物块从圆弧轨道顶端由静止开始滑下，最后从小车右端水平飞出，小物块与小车上表面的动摩擦因数为μ=0.4，g=10m／s2。求：
(1)小物块滑到圆弧轨道底端（最低点）Q时，对轨道的压力；
(2)小物块在小车上运动的时间；
(3)小物块落地的瞬时与小车右端的距离。

参考答案：

解：
(1)设小物块滑到圆弧轨道底端Q的速度vQ，在小物块从圆弧轨道上滑下的过程中，由机械能守恒定律得
mgR=mvQ2／R
小物块在圆弧轨道底端Q，由牛顿第二定律有
N-mg=mvQ2／R
联立解出N=30 N
由牛顿第三定律，小物块对轨道的压力为30 N；
(2)小物块在小车上滑动过程中，小物块 与小车加速度分别为am和aM，对地位移分别为xm和xM，则
am=μmg/m
aM=μmg/M
xm=vQt-amt2/2
xM=aMt2/2
又L=xm-xM
联立解出t=0.5 s
(3)小物块从小车右端水平飞出时，小物块与小车的速度分别为vm=vQ-amt
vM=aMt
又h=gt"2/2
x=（vm-vM）t"
联立解出x=1.2 m。

本题解析：

本题难度：一般

4、选择题  如图所示，一足够长的光滑斜面，倾角为θ，一弹簧上端固定在斜面的顶端，下端与物体b相连，物体b上表面粗糙，在其上面放一物体a。将物体a、b从O点由静止开始释放，释放时弹簧恰好处于自由伸长状态，且在运动的过程中两物体始终保持相对静止。下列描述正确的是(? )

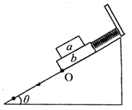
A．在向下运动的过程中，两者加速度始终在减小
B．在向下运动的过程中，a物体受到的摩擦力始终增加
C．当两物体的速度达到最大值时，a物体受到的摩擦力为0
D．当两物体的加速度达到最大值时，a物体受到的摩擦力可能为0

参考答案：BD

本题解析：对于ab整体来说，在向下运动过程中，由于刚开始 重力沿斜面向下的分力大于弹簧的弹力，所以两者先加速，随着物体向下运动弹簧的弹力在不断增加，所以当弹力等于重力沿斜面向下的分力时，加速度为零，再向下运动，弹力大于重力沿斜面的分力，整体做减速运动，所以A错误，当两物体的速度达到最大时，即加速度为零时，a受到重力和支持力，如果摩擦力为零的话，加速度就不为零，所以还要受到一个摩擦力，所以C错误，如果两物体的最大加速度为重力与支持力的合力提供，则a物体受到的摩擦力为零，所以B错误。D正确，

本题难度：简单

5、简答题  如图所示，MN、PQ是平行金属板，板长为L，两板间距离为

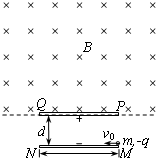
参考答案：


（1）粒子在电场中做类平抛运动如图所示，
设运动时间为t，则有：
垂直场强方向：L=v0t…①
沿场强方向：L2=12at2…②
加速度：a=Eqm…③
电场强度：E=UL2…④
联立?①～④解得：U=mv202q．
（2）设粒子离开电场沿场强方向速度大小为vy，则有：
L2=vy2t…⑤
由数学知识有：
tanθ=vyv0…⑥
联立①⑤⑥式解得：θ=450
（3）粒子在磁场中运动轨迹如图所示，设轨道半径为R，根据牛顿第二定律有：
qvB=mv2R…⑦
运动速度：v=v0cosθ…⑧
由几何知识有：R=L2sinθ…⑨
联立⑦～⑨解得：B=2mv0qL?．
答：（1）两金属板间所加电压U的大小为mv202q．
? （2）从Q处离开电场时的偏转角为450．
? ?（3）匀强磁场的磁感应强度的大小为2mv0qL?．

本题解析：

本题难度：一般