1、计算题 传送带以恒定速度v=4m/s顺时针运行,传送带与水平面的夹角θ=37°.现将质量m=2 kg的小物品轻放在其底端(小物品可看成质点),平台上的人通过一根轻绳用恒力F=20 N拉小物品,经过一段时间物品被拉到离地高为H=1.8m的平台上,如图所示.已知物品与传送带之间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力,g取10m/s2,已知sin37°=0.6,cos37°=0.8.求:
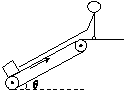
(1)物品从传送带底端运动到平台上所用的时间是多少?
(2)若在物品与传送带达到同速瞬间撤去恒力F,则物品还需多少时间才能离开皮带?
参考答案:(1)1 s (2)(2-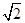 )s
)s
本题解析:(1)物品在达到与传送带速度v=4 m/s相等前,做匀加速直线运动,有:
F+μmgcos37°-mgsin37°=ma1 解得a1=8 m/s2
由v=a1t1得t1=0.5s 位移x1= a1t
a1t =1m
=1m
物品与传送带达到共同速度后,因F-mgsinθ=8 N=μmgcos37°,故物品在静摩擦力作用下随传送带一起匀速上升.位移x2= -x1=2m,t2=
-x1=2m,t2=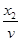 =0.5s
=0.5s
总时间为t=t1+t2=1s
(2)在物品与传送带达到同速瞬间撤去恒力F,则有:μmgcos37°-mgsin37°=ma2
解得:a2=-2m/s2
假设物品能向上匀减速运动到速度为零,则通过的位移为x= =4 m>x2
=4 m>x2
故物品向上匀减速运动未达到速度为零时即已脱离传送带.
由x2=vt3+ a2t
a2t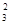 解得t3=(2±
解得t3=(2±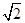 )s 所以t3=(2-
)s 所以t3=(2-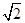 )s
)s
考点:考查了牛顿第二定律,运动学公式的应用
本题难度:困难
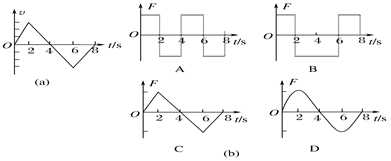
2、选择题 某物体做直线运动的v-t图象如图 (a)所示,据此判断图(b)F表示物体所受合力,t表示物体运动的时间)四个选项中正确的是( )
参考答案:B
本题解析:由图可知前两秒物体做初速度为零的匀加速直线运动,所以前两秒受力恒定,2s-4s做正方向匀减速直线运动,所以受力为负,且恒定,4s-6s做负方向匀加速直线运动,所以受力为负,恒定,6s-8s做负方向匀减速直线运动,所以受力为正,恒定,综上分析B正确.
故选:B.
考点:速度时间图线;匀变速运动的规律.
本题难度:一般
3、实验题 在“探究加速度与质量的关系”的实验中:
(1)备有器材:A.长木板;B.电磁打点计时器、低压交流电源、纸带;C.细绳、小车、砝码;D.装有细沙的小桶;E.薄木板;F.毫米刻度尺;还缺少的一件器材是________.
(2)实验得到如图甲所示的一条纸带,相邻两个计数点的时间间隔为T;B、C
两点的间距x2和D、E两点的间距x4已量出,利用这两段间距计算小车加速度的表达式为______________.
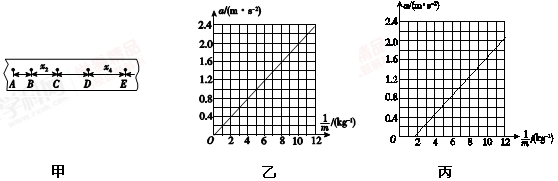
某同学根据实验数据画出的a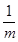 图线如图乙所示,从图线可得沙和沙桶的总质量为________ kg.(g取10 m/s2)
图线如图乙所示,从图线可得沙和沙桶的总质量为________ kg.(g取10 m/s2)
另一位同学根据实验数据画出的a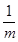 图像如图丙所示,则造成这一结果的原因是
图像如图丙所示,则造成这一结果的原因是
参考答案:(1)天平;(2)(x4-x2)/2T2;(3)0.02(0.018-0.02均可);(4)末平衡摩擦力或平衡摩擦力不够。
本题解析:(1)实验要探究加速度与质量的关系,需要测出小车的质量,所以要用到天平。
(2)对于匀变速运动,相邻的相等时间内的位移差相等,x4-x3=x3-x2=aT2,x4-x2=2aT2,a=(x4-x2)/2T2。
(3)根据F=ma,a=F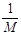 ,a-
,a-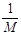 图像的斜率等于F,在m<<M的条件下,F=mg,所以沙和沙桶的总质量为0.02kg。
图像的斜率等于F,在m<<M的条件下,F=mg,所以沙和沙桶的总质量为0.02kg。
(4)根据图像,在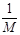 很小,即M很大时,a为零,说明末平衡摩擦力或平衡摩擦力不够。
很小,即M很大时,a为零,说明末平衡摩擦力或平衡摩擦力不够。
考点:探究加速度与质量的关系
本题难度:一般
4、计算题 如图所示,质量M=8.0kg、长L=2.0m的薄木板静置在水平地面上,质量m=0.50kg的小滑块(可视为质点)以速度v0=3.0m/s从木板的左端冲上木板。已知滑块与木板间的动摩擦因数μ=0.20,重力加速度g取10m/s2。

(1)若木板固定,滑块将从木板的右端滑出,求:
a.滑块在木板上滑行的时间t;
b.滑块从木板右端滑出时的速度v。
(2)若水平地面光滑,且木板不固定。在小滑块冲上木板的同时,对木板施加一个水平向右的恒力F,如果要使滑块不从木板上掉下,力F应满足什么条件?(假定滑块与木板之间最大静摩擦力与滑动摩擦力相等)
参考答案:(1)a.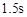 b.1m/s(2)
b.1m/s(2)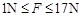
本题解析:(1)a.滑块在木板上做匀减速直线运动,初速度为v0=3.0m/s,位移为L=2.0m。滑块在滑行的过程中受重力、支持力、和摩擦力,其中重力=支持力。根据牛顿第二定律有,滑块加速度的大小
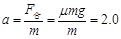 m/s2
m/s2
设滑块在木板上滑行的时间为t,根据运动学公式有
所以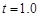 s 或
s 或 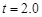 s(舍) (3分)
s(舍) (3分)
之所以要舍去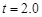 s,是因为如果木板足够长,当
s,是因为如果木板足够长,当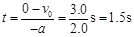 s时,滑块就静止了。
s时,滑块就静止了。
b. m/s (2分)
m/s (2分)
(2)①设当F=F1时,滑块恰好运动到木板的右端,然后与木板一起运动。在滑块与木板有相对滑动的这段时间内,滑块做匀减速直线运动,木板做匀加速直线运动。设这段时间为t1,滑块与木板共同运动的速度为v1,则有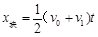 ,
,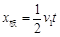 ,
,
所以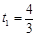 s,
s,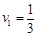 m/s
m/s
所以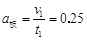 m/s2
m/s2
根据牛顿第二定律有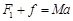
所以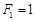 N
N
所以,当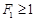 N时,滑块不会从木板的右端滑出 (4分)
N时,滑块不会从木板的右端滑出 (4分)
②当滑块与木板共速后,只要不发生相对滑动,滑块就不会从木板的左端滑出,根据牛顿第二定律:滑块与木板共同运动的加速度 ,而滑块在静摩擦力的作用下,能达到的最大加速度
,而滑块在静摩擦力的作用下,能达到的最大加速度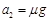 。因此,滑块不从木板左端滑出需满足的条件是
。因此,滑块不从木板左端滑出需满足的条件是 ,即
,即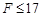 N。 (3分)
N。 (3分)
所以滑块不从木板掉下的条件是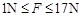 。
。
考点:考查了牛顿第二定律与运动学公式的应用
本题难度:困难
5、选择题 如图,足够大的光滑绝缘水平面上有三个带电质点,A和C围绕B做匀速圆周运动,B恰能保持静止,其中A、C和B的距离分别是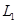 ,和
,和 .不计三质点间的万有引力,则A和C的比荷(电量与质量之比)之比应是
.不计三质点间的万有引力,则A和C的比荷(电量与质量之比)之比应是

A. 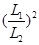 B.
B.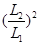 C.
C. 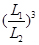 D.
D.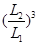
参考答案:C
本题解析:根据B恰能保持静止可得: ;A做匀速圆周运动,根据A受到的合力提供向心力,
;A做匀速圆周运动,根据A受到的合力提供向心力, ,C做匀速圆周运动,
,C做匀速圆周运动, ,联立解得A和C的比荷(电量与质量之比)之比应是
,联立解得A和C的比荷(电量与质量之比)之比应是 ,故选C.
,故选C.
考点:库仑定律及牛顿定律。
本题难度:一般