1、简答题  开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即

参考答案：因行星绕太阳做匀速圆周运动，于是轨道半长轴a即为轨道半径r，根据万有引力定律和牛顿第二定律有
Gm行M太r2=m行(2πT)2r
得：r3T2=K=GM太4π2

本题解析：

本题难度：一般

2、选择题  假设地球一年自转一周（地球自转方向与公转方向一致），下述提法正确的是（　　）
A．赤道上人的体重将增大
B．地球上半年为白天，下半年为黑夜
C．赤道上白天和黑夜将变为无限长
D．赤道上相同圆锥摆的周期将减小

参考答案：A、自转周期变大，则角速度变小，赤道上的人靠重力和支持力的合力提供向心力，向心力减小，知重力加速度增大，则体重增大．故A正确．
B、自转周期变大，则白天和黑夜变为无限长．故B错误，C正确．
D、重力加速度增大，根据单摆的周期公式，知圆锥摆的周期将减小．故D正确．
故选ACD．

本题解析：

本题难度：简单

3、选择题  已知某星球的质量为M，星球的半径为R，引力常量为G，它的一颗卫星绕该星球做匀速圆周运动离星球表面的高度也为R，，则卫星在圆轨道上运行的速率为
A．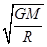
B．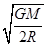
C．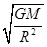
D．

参考答案：B

本题解析：根据万有引力提供向心力可得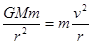，可知，因为星球做匀速圆周运动离星球表面的高度为R，所以轨道半径r=2R，则卫星在圆轨道上运行的速率为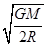
故选B

本题难度：简单

4、选择题  假设地球是一个质量均匀分布的球体，半径为R．在离海平面不同高度的位置，物体所受的重力也略有不同，有人利用这个特点来确定山的高度．他用单摆在海平面处测出摆的周期是T0．在某山顶上测得该单摆周期为T，不考虑地球自转的因素，可求得该山顶离海平面的高度为（　　）
A．

参考答案：设单摆的摆长为L，地球的质量为M，则据万有引力定律可得地面的重力加速度和高度为h时的重力加速度分别为：
g=GMR2，gh=GM(R+h)2
据单摆的周期公式可知T0=2π

本题解析：

本题难度：一般

5、选择题  用火箭将质量为m的卫星送入距离地球表面高度为h的轨道，并使卫星具有速度v，假设卫星的重力随高度的变化可以忽略，则关于外力对卫星做功的情况，以下判断正确的是（　　）
A．卫星克服重力做功为?mgh
B．卫星克服重力做功为?mgh+

参考答案：A、B、卫星重力大小几乎不变，重力势能增加mgh，故克服重力做功为mgh，故A正确，B错误；
C、火箭的推力对卫星做功等于卫星机械能增加量，为mgh+12mv2，故C错误；
D、合外力对卫星做功等于卫星动能增加量，故等于12mv2，故D正确；
故选AD．

本题解析：

本题难度：简单