1、计算题 (9分)如图所示,在水平光滑桌面上放一质量为2m的玩具小车,在小车的左侧固定一光滑圆弧轨道(是小车的一部分),其末端处为水平。用手将小车固定在桌面上,然后将质量为m的小球从光滑圆弧轨道某位置由静止释放,小球离开轨道后落在车上A点,OA=s。若小车不固定时,将该小球从光滑圆弧轨道同一位置由静止释放,则小球将落在车上O点多远处? (设小车足够长,球不致落在车外)

参考答案:s1=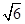 s /2
s /2
本题解析:当小车固定不动时,设小球离开轨道水平部分时的速度大小为v,从离开水平轨道到落到车上A点所花时间为t,有s="vt"
当小车不固定时,设小球离开轨道水平部分时相对于地面的速度的大小为v1,车速的大小为v2,由动量守恒定律,mv1=2mv2
由机械能守恒定律,两次小球离开轨道水平部分时的总动能相同,
则有:mv12/2+2mv22/2=mv2/2
设小球落在车上A"处,OA"=s1,则由平抛运动规律可知:s1=(v1+v2)t
解得:s1=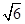 s /2
s /2
本题难度:一般
2、选择题 如图5-2-10所示,在一光滑的水平面上有两块相同的木板B和C.重物A(视为质点)位于B的右端,A、B、C的质量相等,现A和B以同一速度滑向静止的C,B与C发生正碰.碰后B和C黏在一起运动,A在C上滑行,A与C有摩擦力.已知A滑到C的右端而未掉下.试问:从B、C发生正碰到A刚移动到C右端期间,C所走过的距离是C板长度的多少倍?

图5-2-10
参考答案: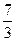
本题解析:设A、B、C的质量均为m.碰撞前,A与B的共同速度为v0,碰撞后B与C的共同速度为v1.对B、C构成的系统,由动量守恒定律得mv0=2mv1?①
设A滑至C的右端时,三者的共同速度为v2,对A、B、C三者构成的系统,由动量守恒定律得2mv1=3mv2?②
设A与C的动摩擦因数为μ,从发生碰撞到A移至C的右端时,C所走过的距离为s,对B、C,由功能关系
μmgs=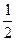 (2m)v22-
(2m)v22-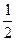 (2m)v12?③
(2m)v12?③
设C的长度为l,对A,由功能关系μmg(s+l)=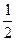 mv02-
mv02-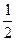 mv22?④
mv22?④
由以上四式解得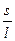 =
=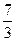 .
.
本题难度:简单
3、其他
参考答案: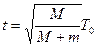
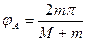
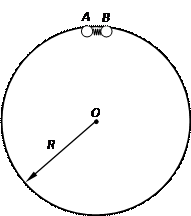
本题解析:A固定释放弹簧后,B做匀速圆周运动
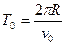 ①
①
弹簧的弹性势能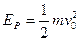 ②
②
A、B均不固定,弹簧释放过程动量守恒、能量守恒
 ③
③
 ④
④
设分离后经过时间t两球第一次相遇,则
 ⑤
⑤
解得: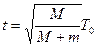 ⑥
⑥
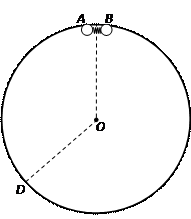
A、B分离后均做匀速圆周运动,设A、B分离到D点第一次相遇两球转过的角度分别为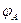 、
、 ,如图所示,则有:
,如图所示,则有:
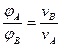 ⑦ 由
⑦ 由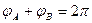 ⑧
⑧
解得: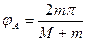 ⑨
⑨
评分标准:本题共20分。正确得出⑤、⑥式各给3分,正确得出其①、②、③、④、⑦、⑧、⑨式各给2分。
本题难度:一般
4、选择题 三木块从同一高度同时开始自由下落,其中木块甲自由落体;木块乙在刚刚开始下落时被一颗子弹沿水平方向击中并留在其中;木块丙在下落途中被一颗子弹沿水平方向击中并留在其中。不计空气阻力及子弹进入木块的时间,则(?)
A.三块木块同时落地
B.甲木块最先落地,乙、丙同时落地
C.木块丙最后落地,甲、乙同时落地
D.甲、乙、丙依次先后落地
参考答案:C
本题解析:略
本题难度:简单
5、简答题 在光滑水平面上有一辆平板车,质量分别为m1、m2的两人站在车的两端(如图所示),他们以对地速度v1、v2相向而行,则在下列三情况下,车的运动方向如何?

(1)m1=m2,v1=v2;
(2)m1≠m2,v1=v2;
(3)m1=m2,v1≠v2.
参考答案:(1)平板车不动.
(2)m2>m1时,平板车向右运动;
m2<m1时,平板车向左运动.
(3)v2>v1时,平板车向右运动;
v2<v1时,平板车向左运动.
本题解析:以m1、m2和车为系统,规定v1方向为正方向、设车质量为M.由动量守恒,得
m1v1-m2v2+Mv=0
(1)当m1=m2、v1=v2时,得v=0,所以平板车不动.
(2)当v1=v2、m2>m1时,得v>0,所以平板车向右运动;
当v1=v2、m2<m1时,得v<0,所以平板车向左运动.
(3)当m1=m2、v2>v1时,得v>0,所以平板车向右运动;
当m1=m2、v2<v1时,得v<0,所以平板车向左运动.
本题难度:简单