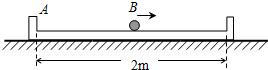
1、填空题  如图，A为内壁长为2m的U型框，框内有一小球B．某时刻开始，小球从框的中点以1m/s的速度向右匀速直线运动，与框右侧挡板碰撞后立刻以相等的速度返回，以后的每次碰撞小球只改变速度方向，且不计碰撞时间．
（1）若框始终静止，则4s内小球与框碰撞的次数为______次．
（2）若框始终以0.5m/s的速度向右匀速直线运动，则3s末小球与框左侧挡板的距离为______m．

参考答案：（1）4s内小球的路程wei：s=v球t=1m/s×4s=4m，
框静止不动，小球从中点开始向右运动，在4s内的路程为4m，小球运动1m与框发生第一次碰撞，在经过2m，共运动1m+2m=3m与框发生第二次碰撞，要发生第三次碰撞需要在运动2m，小球需一共需要运动3m+2m=5m，
在4s内小球运动了4m，因此在4s内小球与框碰撞2次；
（2）小球与框同时向右运动，小球与框的右侧发生第一次碰撞的时间：
t1=s′v小球-v框=11-0.5=2s，
与框碰撞后，小球返回，向左运动，再经过1s小球的路程：
s=v球t=1m/s×s=1m，
框的路程：s′=v框t=0.5m/s×1s=0.5m，
此时小球与框左侧挡板的距离为：
2m-1m-0.5m=0.5m，
即3s末小球与框左侧挡板的距离为0.5m；
故答案为：2；0.5．

本题解析：

本题难度：简单

2、计算题  如图，一质量为m的物块A静止于光滑水平面上，一根轻质弹簧一端固连在A上，另一端与固定在水平面上的测力计相连．通过测力计可以测出弹簧产生的压力的大小．一质量为m的物块B以速度v0与A相碰后一起向右运动，当它们速度为零时，测力计的读数为F．若B的质量为2m，以v0的速度与A碰后一起运动，当测力计的读数仍为F时，求它们速度的大小。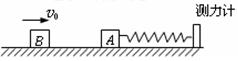

参考答案：质量为m的物块B与A相碰后的速度为v1，根据动量守恒定律
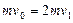? 4分
A、B速度为零时，弹簧的弹性势能为Ep
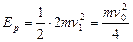? 4分
质量为2m的物块B与A相碰后的速度为v2，根据动量守恒定律
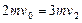? 4分
当测力计的读数为F时，弹簧的弹性势能仍为Ep，此时A、B速度为v
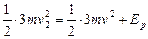? 4分
? 2分

本题解析：略

本题难度：一般

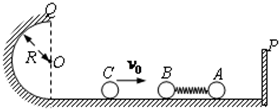
3、简答题  可视为质点的小球A、B静止在光滑水平轨道上，A的左边固定有轻质弹簧，B与弹簧左端接触但不拴接，A的右边有一垂直于水平轨道的固定挡板P．左边有一小球C沿轨道以某一初速度射向B球，如图所示，C与B发生碰撞并立即结成一整体D，在它们继续向右运动的过程中，当D和A的速度刚好相等时，小球A恰好与挡板P发生碰撞，碰后A立即静止并与挡板P粘连．之后D被弹簧向左弹出，D冲上左侧与水平轨道相切的竖直半圆光滑轨道，其半径为R=0.6m，D到达最高点Q时，D与轨道间弹力F=2N．已知三小球的质量分别为mA=0.2kg、mB=mC=0.1kg．取g=10m/s2，求：
（1）D到达最高点Q时的速度vQ的大小
（2）D由Q点水平飞出后的落地点与Q点的水平距离s
（3）C球的初速度v0的大小．

参考答案：解 （1）D在Q点时据牛顿第二定律有F+mDg=mDvQ2R
解得：vQ=

本题解析：

本题难度：一般

4、计算题  如图所示，三个质量均为m的弹性小球用两根长均为L的轻绳连成一条直线而静止在光滑水平面上。现给中间的小球B一个水平初速度v0，方向与绳垂直。小球相互碰撞时无机械能损失，轻绳不可伸长。求：
(1)当小球A、C第一次相碰时，小球B的速度；
(2)当三个小球再次处在同一直线上时，小球B的速度；
(3)运动过程中小球A的最大动能EKA和此时两根绳的夹角θ；
(4)当三个小球处在同一直线上时，绳中的拉力F的大小。

参考答案：解：（1）设小球A、C第一次相碰时，小球B的速度为vB，考虑到对称性及绳的不可伸长特性，小球A、C沿小球B初速度方向的速度也为vB，由动量守恒定律，得

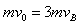
由此解得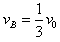
（2）当三个小球再次处在同一直线上时，则由动量守恒定律和机械能守恒定律，得


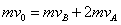
解得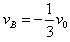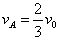，（三球再次处于同一直线）
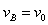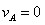，（初始状态，舍去）
所以，三个小球再次处在同一直线上时，小球B的速度为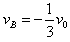（负号表明与初速度反向）
（3）当小球A的动能最大时，小球B的速度为零。设此时小球A、C的速度大小为u，两根绳间的夹角为θ（如图），则仍由动量守恒定律和机械能守恒定律，得
?


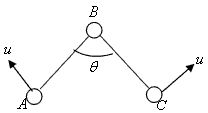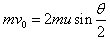
另外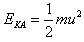
由此可解得，小球A的最大动能为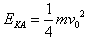，此时两根绳间夹角为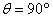
（4）小球A、C均以半径L绕小球B做圆周运动，当三个小球处在同一直线上时，以小球B为参考系（小球B的加速度为0，为惯性参考系），小球A（C）相对于小球B的速度均为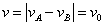
所以，此时绳中拉力大小为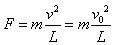

本题解析：

本题难度：困难

5、选择题  如图，光滑水平面上有大小相同的A、B两球在同一直线上运动．两球质量关系为mB＝2 mA，规定向右为正方向，A、B两球的动量均为6 kg·m/s，运动中两球发生碰撞，碰撞后A球的动量增量为－4 kg·m/s.则(　　)
A．左方是A球，碰撞后A、B两球速度大小之比为2∶5
B．左方是A球，碰撞后A、B两球速度大小之比为1∶10
C．右方是A球，碰撞后A、B两球速度大小之比为2∶5
D．右方是A球，碰撞后A、B两球速度大小之比为1∶10

参考答案：A

本题解析：同向运动的两个小球发生碰撞，则后面的小球的速度一定减小，前面的小球速度一定增大，所以左方是Ａ球，右方是Ｂ球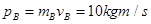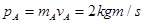，，，又知道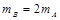，可得碰撞后A、B两球速度大小之比为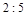，所以Ａ正确。

本题难度：简单