1、简答题  长L=0.5m的轻杆，其一端连接着一个零件A，A的质量m=2kg．现让A在竖直平面内绕O点做匀速圆周运动，如图所示．在A通过最高点时，求下列两种情况下A对杆的作用力．（g=10m/s2）：
（1）A的速率为1m/s；
（2）A的速率为4m/s．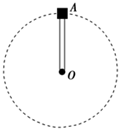

参考答案：以A为研究对象，设其受到杆的拉力为F，则有
mg+F=mv2L．
（1）代入数据v=1?m/s，可得
F=m（v2L-g）=2×（120.5-10）N=-16?N，
即A受到杆的支持力为16?N．根据牛顿第三定律可得A对杆的作用力为压力16?N．
（2）代入数据v=4?m/s，可得
F=m（v2L-g）=2×（420.5-10）N=44?N，
即A受到杆的拉力为44?N．根据牛顿第三定律可得A对杆的作用力为拉力44?N．
答：（1）A的速率为1m/s，A对杆的作用力为压力16 N．
（2）A的速率为4m/s，A对杆的作用力为拉力44 N．

本题解析：

本题难度：一般

2、简答题  如图所示，在平面坐标系xOy内，同种带正电离子，质量m=1.0×10-20kg、带电量q=1.0×10-10C，以相同速度不断从C点垂直射入匀强电场，偏转后通过极板MN上的小孔O离开电场时的速度大小为v=2.0×106m/s，方向与x轴成30°角斜向上．在y轴右侧有一个圆心位于O"（0.01m，0）点，半径r=0.01m的圆形磁场区域，磁场方向垂直纸面向外，磁感应强度B=0.01T，有一垂直于x轴的面积足够大的竖直荧光屏PQ置于坐标x0=0.04m处．已知NC之间的距离d=0.02m．试求：
（1）粒子在磁场中的运动轨迹半径；
（2）偏转电场强度的大小；
（3）若圆形磁场区可沿x轴移动，圆心O"在x轴上的移动范围为（0.01m，+∞），由于磁场位置的不同，导致粒子打在荧光屏上的位置也不同，求粒子打在荧光屏上点的纵坐标的范围．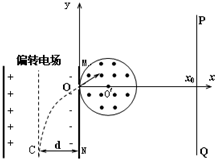

参考答案：（1）离子在磁场中做匀速圆周运动，由于洛仑兹力提供向心力，则有：qvB=mv2R?①
解得：R=0.02m?
（2）将速度v分解为如图所示的x方向速度v1和y方向速度v2，
得到：v2=vsin30°=0.5v?②
则初速度为v0=vc ③
离子在偏转电场中，由动能定理：Eqd=12mv2-12mv?22? ?④
联立②③④解得：E=7.5×103V/m?
（3）当圆心O′在x=0.01m时，由于R=0.02m=2r，所以离子从x轴上的D点离开磁场．?
由几何关系可知，离子打在荧光屏的最低点，纵坐标为：y1=-（x0-2r）tan30°=2

本题解析：

本题难度：一般

3、简答题  如图甲所示，真空中两水平放置的平行金属板C、D，上面分别开有两对正对的小孔O1、O2和O3、O4，O2与O3之间的距离d=20cm．金属板C、D接在正弦交流电源上，C、D两板间的电压UCD随时间t变化的图线如图乙所示．t=0时刻开始，从C板小孔O1处连续不断飘入质量m=3.2×10-25kg、电荷量q=1.6×10-19C的带正电的粒子（飘入速度很小，可忽略不计）．在D板外侧有范围足够大匀强磁场，磁感应强度大小B=0.1T，方向垂直纸面向里，粒子受到的重力及粒子间的相互作用力均可忽略不计，平行金属板C、D之间距离足够小，粒子在两板间的运动时间可忽略不计．（取π近似等于3）

（1）带电粒子若经磁场的作用后恰能进入小孔O3，则带电粒子从小孔O2进入磁场时的速度为多大？
（2）在什么时刻飘入小孔O1的粒子，恰好能够进入小孔O3？
（3）经过小孔O3进入C、D两板间的粒子，从小孔O4射出时的动能为多大？

参考答案：（1）设带电粒子小孔O2进入磁场时的速度为v0，粒子在磁场中做匀速圆周运动，其半径为R，根据牛顿第二定律有qv0B=mv02R
因粒子恰好能进入小孔O3，粒子运动轨迹如答图2所示，有R=12d
解得速度v0=qBd2m=5×103m/s
（2）设恰能进入小孔O3的粒子在电场中运动时CD板对应的电压为U0，根据动能定理qU0=12mν02
解得U0=mν022q=25V
由于粒子带正电，因此只有在C板电势高（UCD=UC-UD＞0）时才能被加速进入磁场，因此解得UCD=25?V对应时刻分别为
t1=（0.25+2n）×10-4s?（n=0，1，2…）
t2=（0.75+2n）×10-4s?（n=0，1，2…）
（3）设粒子在磁场中运动的周期为T，根据牛顿第二定律和圆周运动规律qv0B=4π2mRT2，v0=2πRT
得T=2πmqB
粒子在磁场中运动的时间t=T2=πmqB=0.6×10-4s
在t1时刻飘入的粒子，经过时间t，粒子到达小孔O3时，C、D两板间的电压为UCD=15V．粒子在两板之间做减速运动，设到达小孔O4时的动能为E1，根据动能定理，得
-qUCD=E1-12mv20
解得E1=1.6×10-18J
在t2时刻飘入的粒子，经时间t，粒子到达小孔O3时，C、D两板间的电压为UCD′=-35V．粒子在两板之间做加速速运动，设到达小孔O4时的动能为E2，根据动能定理，得
-qUCD′=E2-12mv20
解得E2=9.6×10-18J
答：（1）带电粒子从小孔O2进入磁场时的速度为v0=5×103m/s；
（2）解得UCD=25V，对应时刻分别为
t1=（0.25+2n）×10-4s（n=0，1，2…）
t2=（0.75+2n）×10-4s（n=0，1，2…）
（3）经过小孔O3进入C、D两板间的粒子，从小孔O4射出时的动能为E2=9.6×10-18J．

本题解析：

本题难度：一般

4、填空题  一个质量为m电荷量为q的带正电粒子从x轴上的P（a，0）点以速度v，沿与x正方向成60°的方向射入第一象限内的匀强磁场中，并恰好垂直于y轴射出第一象限．则匀强磁场的磁感应强度B大小为______，射出点的坐标为______．

参考答案：如图所示，由射入、射出点的速度方向可找出圆心O，并得出半径为r=2a

本题解析：

本题难度：一般

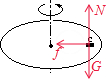
5、选择题  A、B、C三个物体放在旋转圆台上，都没有滑动，如图所示．静摩擦因素均为μ，A的质量为2m，B、C的质量均为m，A、B离轴为R，C离轴为2R．当圆台旋转时，下列说法错误的是（　　）
A．当圆台匀速转动时，C物的向心加速度最大
B．当圆台匀速转动时，B的静摩擦力最小
C．当圆台转速逐渐增加时，A受到的静摩擦力始终指向圆台的转轴
D．当圆台转速增加时，C比A先滑动

参考答案：A、B三个物体都做匀速圆周运动，静摩擦力提供向心力，则静摩擦力指向圆心．
对任意一个受力分析，如图，支持力与重力平衡，则
F合=f=F向
由于a、b、c三个物体共轴转动，角速度ω相等，
根据题意，rc=2ra=2rb=2R
由向心力公式F向=mω2r，得三物体所受的静摩擦力大小分别为：
fA=2mω2R
fB=mω2R
fC=mω2（2R）=2mω2R，所以B的静摩擦力最小．
三个物体的向心加速度分别为：
aA=ω2R，aB=ω2R，aC=mω2（2R）=2ω2R，所以C物的向心加速度最大．故A、B正确；
C、当圆台转速逐渐增加时，A受到的静摩擦力应有切向的分力，还有径向的分力，所以静摩擦力不指向圆台的转轴，故C错误．
D、对任意一物体，由于摩擦力提供向心力，有μmg=mω2r
当ω变大时，所需要的向心力也变大，当达到最大静摩擦力时，物体开始滑动，
当转速增加时，A、C所需向心力同步增加，且保持相等，由最大静摩擦力公式fm=μmg知，C的最大静摩擦力小，C比A先滑动．故D正确；
本题选错误的，故选：C．

本题解析：

本题难度：一般