1、选择题 如图所示,水平地面上有一个坑,其竖直截面为半圆,O为圆心,且AB为沿水平方向的直径,圆弧上有一点C,且∠COD=600。若在A点以初速度v1沿AB方向平抛一小球,小球将击中坑壁上的最低点D;若在C点以初速度v2沿BA方向平抛的小球也能击中D点。重力加速度为g,下列说法正确的是(? )

A.抛出时,两球的速度大小之比为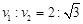
B.抛出时,两球的速度大小之比为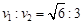
C.运动到D点时,两球的速度方向的夹角为60°
D.若两球同时抛出且速度大小合适,则两球可能在空中相遇
参考答案:B
本题解析:设圆半径为r,根据平抛运动规律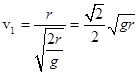 ,
,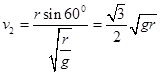
抛出时,两球的速度大小之比为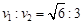 ,B正确,A错误,两球球与水平方向的夹角
,B正确,A错误,两球球与水平方向的夹角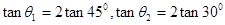 ,所以两球在D点的速度方向大于60,C错误,如果要使两球在空中相遇在相同的时间内在竖直方向上必须满足,A球下落高度必须大于
,所以两球在D点的速度方向大于60,C错误,如果要使两球在空中相遇在相同的时间内在竖直方向上必须满足,A球下落高度必须大于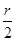 ,而B球的高度小于
,而B球的高度小于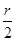 ,所以是不可能的,无论抛出速度大小如何,都不会满足相遇条件的,D错误,
,所以是不可能的,无论抛出速度大小如何,都不会满足相遇条件的,D错误,
本题难度:一般
2、选择题 如图所示,两个质量相等的物体A、B处在同一水平线上,当物体A被水平抛出的同时,物体B开始自由下落,图中曲线AC为物体A的运动轨迹,直线BD为物体B的运动轨迹,两轨迹相交于O点,空气阻力忽略不计,则
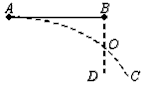
[? ]
A.两物体在O点时的速度相同
B.两物体在O点相遇
C.两物体在O点时的动能相等
D.两物体在O点时重力的功率相等
参考答案:BD
本题解析:
本题难度:一般
3、选择题 从某一高度以相同速度相隔1s先后水平抛出甲、乙两个小球,不计空气阻力,在乙球抛出后两球在空中运动的过程中,下述说法正确的是:
A.两球水平方向的距离越来越大
B.两球竖直高度差越来越大
C.两球水平方向的速度差越来越大
D.两球每秒内的速度变化量相同,与其质量无关
参考答案:BD
本题解析:水平方向上做匀速直线运动,所以水平距离不变.A错误;
平抛运动在竖直方向上做自由落体运动,设乙抛出时开始计时,甲在竖直方向上的位移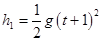 ,乙在竖直方向上的位移
,乙在竖直方向上的位移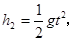 ?两球的高度差
?两球的高度差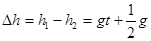 随时间增大越来越大.故B正确.
随时间增大越来越大.故B正确.
平抛运动在水平方向上做匀速直线运动,速度差为0.故C错误.
平抛运动是加速度不变的曲线运动,根据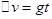 知,每秒钟速度的变化量相同,方向竖直向下,与质量无关.故D正确.
知,每秒钟速度的变化量相同,方向竖直向下,与质量无关.故D正确.
故选BD.
点评:解决本题的关键知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.以及知道平抛运动是加速度不变的曲线运动,每秒钟速度的变化量相同,方向竖直向下.
本题难度:一般
4、计算题 (8分)如图所示,飞机离地面高度为H=500m,飞机的水平飞行速度为v1=100m/s,追击一辆速度为v2=20m/s同向行驶的汽车,欲使炸弹击中汽车,飞机应在距离汽车的水平距离多远处投弹?(不考虑空气阻力,g取10m/s2。)
参考答案: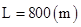
本题解析:解:(1)炸弹从出发到击中汽车的时间为t
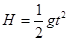 ?
?
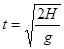 ? 1分
? 1分
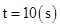 ? 1分
? 1分
炸弹水平方向位移为x1
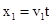 ? 1 分
? 1 分
 ? 1分
? 1分
汽车在水平方向上的位移为x2
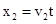 ? 1 分
? 1 分
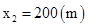 ? 1分
? 1分
飞机投弹时距离汽车的水平距离为L
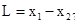 ? 1分
? 1分
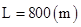 ? 1分
? 1分
本田考查的是平抛运动的问题。平抛运动水平方向匀速直线运动,竖直方向自由落体运动。运用此规律便可解出此题。
本题难度:简单
5、简答题 如图所示,静放在水平面上的
圆形(半径为R)光滑管道ABC,C为最高点,B为最低点,管道在竖直面内.管道内放一小球,小球可在管道内自由移动,现用一装置将小球锁定在P点,过P点的半径OP与竖直方向的夹角为θ.现对管道施加一水平向右的恒力F,同时解除对小球的锁定,管道沿水平面向右做匀加速运动,小球相对管道仍保持静止.经过一段时间后管道遇一障碍物突然停止运动,小球能到达管道的A点.重力加速度为g,小球大小及管道内释不计.求.
(1)恒力作用下圆形管道运动的加速度;
(2)圆形管道从开始运动到突然停止过程中运动距离的可能值.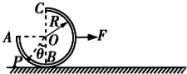
参考答案:
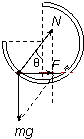
(1)小球受力如图,由力的平行四边形定则及牛顿第二定律得:
mgtanθ=ma;
解得a=gtanθ;
即为恒力作用下的圆形管道运动的加速度;
(2)设圆形管道在运动过程中突然停止前进的速度为v,由匀变速直线运动公式得:v2=2as;
圆形管道停止时,小球沿管道半径方向的速度变为零,沿切线方向的速度保持不变,对速度v沿切向和径向进行分解,则小球速度变为v′=vcosθ;
小球能运动到管道右侧圆心上方至最高点C之间的区域则可返程到达A点,或从C点飞出做平抛运动到达A点;
若小球能运动到管道右侧圆心上方至最高点C之间的区域,则由机械能守恒得:
12m(vcosθ)2=mg(Rcosθ+h),其中0≤h<R
联立以上相关各式得:Rsinθ≤s<2R(1+cosθ)sin2θ
若小球从C点飞出做平抛运动到达A点,则由机械能守恒及平抛运动的规律得:
R=12gt2,R=vCt
12m(vcosθ)2=mgR(1+cosθ)+12mvc2
联立以上相关各式得:s=R(5+4cosθ)2sin2θ
圆形管道从开始运动到突然停止过程中运动距离的可能值为:
Rsinθ≤s<2R(1+cosθ)sin2θ及s=R(5+4cosθ)2sin2θ
本题解析:
本题难度:一般
It is easier to fight for principles than to live up to them. 为原则而斗争容易,按原则的要求活着难.