1、计算题  在高能物理研究中，粒子加速器起着重要作用，而早期的加速器只能使带电粒子在高压电场中加速一次，因而粒子所能达到的能量受到高压技术的限制。1930年，Earnest O. Lawrence博士提出了回旋加速器的理论，他设想用磁场使带电粒子沿圆弧形轨道旋转，多次反复地通过高频加速电场，直至达到高能量，图甲为他设计的回旋加速器的示意图。它由两个铝制D型金属扁盒组成，两个D形盒正中间开有一条狭缝，两个D型盒处在匀强磁场中并接有高频交变电压。图乙为俯视图，在D型盒上半面中心S处有一正离子源，它发出的正离子，经狭缝电压加速后，进入D型盒中，在磁场力作用下运动半周，再经狭缝电压加速；为保证粒子每次经过狭缝都被加速，应设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致。如此周而复始，最后到达D型盒的边缘，获得最大速度后被束流提取装置提取。设被加速的粒子为质子，质子的电荷量为q，质量为m，加速时电极间电压大小恒为U，磁场的磁感应强度为B，D型盒的半径为R，狭缝之间的距离为d，质子从离子源出发时的初速度为零，分析时不考虑相对论效应。
（1）求质子经第1次加速后进入一个D形盒中的回旋半径与第2次加速后进入另一个D形盒后的回旋半径之比；
（2）若考虑质子在狭缝中的运动时间，求质子从离开离子源到被第n次加速结束时所经历的时间；
（3）若要提高质子被此回旋加速器加速后的最大动能，可采取什么措施？
（4）若使用此回旋加速器加速氘核，要想使氘核获得与质子相同的最大动能，请你通过分析，提出一个简单可行的办法。

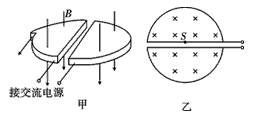
参考答案：解：（1）设质子经过窄缝被第n次加速后速度为vn，
由动能定理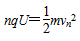? ①
第n次加速后质子在磁场中做匀速圆周运动的半径为Rn，
由牛顿第二定律? ②
由以上两式解得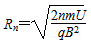
则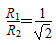
（2）由牛顿第二定律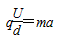? ③
质子在狭缝中经n次加速的总时间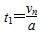 ④
联立①③④解得电场对质子加速的时间?
质子在磁场中做匀速圆周运动的周期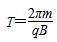 ⑤
粒子在磁场中运动的时间t2＝(n－1) ⑥
联立⑤⑥解得
故质子从离开离子源到被第n次加速结束时所经历的时间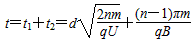
（3）设质子从D盒边缘离开时速度为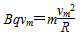，⑦
质子获得的最大动能为 ⑧
所以，要提高质子被此回旋加速器加速后的最大动能，可以增大加速器中的磁感应强度B。
（4）若加速氘核，氘核从D盒边缘离开时的动能为Ek′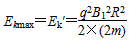， ⑨
联立⑧⑨解得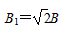，即磁感应强度需增大为原来的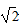倍
高频交流电源的周期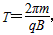，由质子换为氘核时，交流电源的周期应为原来的倍。

本题解析：

本题难度：困难

2、选择题  (2009·淄博一模)如图所示，两虚线之间的空间内存在着正交或平行的匀强电场E和匀强磁场B，有一个带正电的小球(电荷量为＋q，质量为m)从电磁复合场上方的某一高度处自由落下，那么，带电小球可能沿直线通过的电磁复合场是? (　　)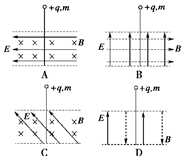

参考答案：CD

本题解析：在A图中刚进入复合场时，带电小球受到方向向左的电场力、向右的洛伦兹力、竖直向下的重力，在重力的作用下，小球的速度要变大，洛伦兹力也会变大，所以水平方向受力不可能总是平衡，A选项错误；B图中小球要受到向下的重力、向上的电场力、向外的洛伦兹力，小球要向外偏转，不可能沿直线通过复合场，B选项错误；C图中小球受到向下的重力、向右的洛伦兹力、沿电场方向的电场力，若这三个力的合力正好为0，则小球将沿直线通过复合场，C选项正确；D图中小球只受到向下的重力和向上的电场力，都在竖直方向上，小球可能沿直线通过复合场，D选项正确．

本题难度：一般

3、选择题  如图一混合正离子束先后通过正交电场磁场区域Ⅰ和匀强磁场区域Ⅱ，如果这束正离子束流在区域Ⅰ中不偏转，进入区域Ⅱ后偏转半径又相同，则说明这些正离子具有相同的

[? ]
A、速度　　　　
B、质量 　　
C、电荷　　　　
D、荷质比

参考答案：AD

本题解析：

本题难度：一般

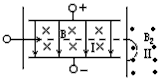
4、选择题  带电质点在匀强磁场中运动，某时刻速度方向如图所示，所受的重力和洛伦兹力的合力恰好与速度方向相反，不计阻力，则在此后的一小段时间内，带电质点将

[? ]
A．可能做直线运动
B．可能做匀减速运动
C．一定做曲线运动
D．可能做匀速圆周运动

参考答案：C

本题解析：

本题难度：一般

5、计算题  （15分）如图甲所示，空间存在B=0.5T，方向竖直向下的匀强磁场，MN、PQ是处于同一水平面内相互平行的粗糙长直导轨，间距L=0.2m， R是连接在导轨一端的电阻，ab是跨接在导轨上质量为m=0.1kg的导体棒。从零时刻开始，通过一小型电动机对ab棒施加一个牵引力F，方向水平向左，使其从静止开始沿导轨做加速运动，此过程中棒始终保持与导轨垂直且接触良好。图乙是棒的v-t图象，其中OA段是直线，AC是曲线，DE是曲线图象的渐进线，小型电动机在12s末达到额定功率P=4.5W，此后保持功率不变。除R外，其余部分电阻均不计，g=10m/s2。

（1）求导体棒ab在0－12s内的加速度大小
（2）求导体棒ab与导轨间的动摩擦因数及电阻R的值
（3）若t=17s时，导体棒ab达最大速度，从0－17s内共发生位移100m，试求12s－17s内，R上产生的热量是多少？

参考答案：（1）0.75m/s2（2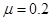）?R=0.4Ω（3）

本题解析：（1）由v-t图象的斜率得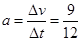m/s2=0.75m/s2
（2）t1=12s时，由v-t图象得速度为 v1="9m/s"
因为，，,
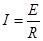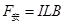
由牛顿第二定律得?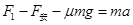即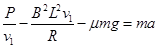
由图象知17s末导体棒ab的最大速度为v2=10m/s，此时加速度为零，同理有
?
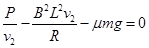联立解得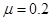?，R=0.4Ω
（3）由v-t图象知0－12s内，导体棒匀加速运动的位移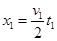=54m
12－17s内，导体棒的位移 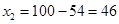m
由能量守恒得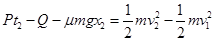
代入数据解得R上产生的热量? Q="12.35" J

本题难度：一般