1、计算题  月球环绕地球运动的轨道半径约为地球半径的60倍，其运行周期约为27天．现应用开普勒定律计算：在赤道平面内离地面多高时，人造地球卫星可随地球一起转动，就像其停留在天空中不动一样．若两颗人造卫星绕地球做圆周运动，周期之比为1∶8，则它们轨道半径之比是多少？(已知R地＝6.4×103 km)

参考答案：3.63×104 km　1∶4

本题解析：月球和人造地球卫星都在环绕地球运转，根据开普勒第三定律，它们运行轨道的半径的三次方跟圆周运动周期的二次方的比值都是相等的．设人造地球卫星运动的半径为R，周期为T＝1天，根据开普勒第三定律有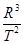：＝k，同理设月球轨道半径为R′，周期为T′，也有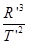＝k
由以上两式可得＝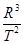
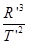
R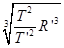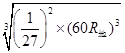＝＝＝6.67R地
在赤道平面内离地面高度
H＝R－R地＝6.67R地－R地＝5.67R地
＝5.67×6.4×103 km＝3.63×104 km.
由开普勒第三定律：＝
又因为T1∶T2＝1∶8，解得R1∶R2＝1∶4.

本题难度：一般

2、选择题  随着航天技术的发展，在地球周围有很多人造飞行器，其中有一些已超过其设计寿命且能量耗尽．每到太阳活动期，地球的大气层会变厚，这时有些飞行器在大气阻力的作用下，运行的轨道高度将逐渐降低（在其绕地球运动的每一周过程中，轨道高度变化很小均可近似视为匀速圆周运动）．为了避免飞行器坠入大气层后对地面设施及人员造成安全威胁，人们设想发射导弹将其在运行轨道上击碎．具体设想是：在导弹的弹头脱离推进装置后，经过一段无动力飞行，从飞行器后下方逐渐接近目标，在进入有效命中距离后引爆弹头并将该飞行器击碎．对于这一过程中的飞行器及弹头，下列说法中正确的是（　　）
A．飞行器轨道高度降低后，它做圆周运动的速率变大
B．飞行器轨道高度降低后，它做圆周运动的周期变大
C．弹头在脱离推进装置之前，始终处于失重状态
D．弹头引爆前瞬间，弹头的加速度一定小于此时飞行器的加速度

参考答案：A、根据万有引力提供向心力得：
GMmR2=mv2R
解得：v=

本题解析：

本题难度：一般

3、选择题  下表是火星和地球部分数据对照表，把火星和地球视为匀质理想球体，它们绕太阳的运动近似看作匀速圆周运动，从表中数据可以分析得出不正确的是（?）

参考答案：C

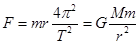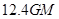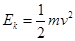本题解析：据题意，向心力为：，将数据代入后发现火星向心力为，地球的为：较大，故A选项正确；公转动能为：，火星动能为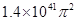：，地球动能为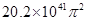：，则地球公转动能较大，B选项正确；第一宇宙速度为：,火星第一宇宙速度为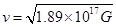：,地球第一宇宙速度为：，则地球第一宇宙速度较大，则C选项错误；星球表面重力加速度为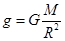：，火星表面重力加速度为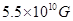：，地球表面重力加速度为：，则地球表面重力加速度较大，D选项正确；据题意应选择C选项。

本题难度：一般

4、简答题  
（1）已知地球半径为R，地球表面重力加速度为g，地球自转周期为T0，请用以上物理量表示“风云二号”D气象卫星的轨道半径r，加速度a 以及线速度v ；
（2）取R=6400km，g=10m/s2，π2=10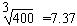，，求出“风云二号”D气象卫星的轨道半径r；
（3）根据第（2）问的结果，定性说明“风云二号”D气象卫星的加速度与随地球一块转动的赤道上物体的加速度的大小关系。

参考答案：
(1) 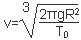?(2) 4.25×104km
(3)风云二号”D卫星的加速度大于赤道上随地球一块自转的物体的向心加速度

本题解析：（1）由题意知，“风云二号”D气象卫星为地球同步静止卫星，其运行周期和地球自转周期相等为T0，由万有引力提供向心力有方程式：
?
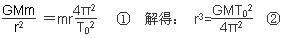又对地球表面的物体m"，地球对它的万有引力与重力相等：
?得：GM=gR2③

（2）将题中数据代入④式得：
?
=4.25×104km?（4分）
（3）“风云二号”D卫星与赤道上随地球一块自转的物体同做圆周运动，且有一样的周期，由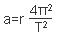知，T相同时，r越大，则a越大，通过第（2）问的计算结果表明r>R，则“风云二号”D卫星的加速度大于赤道上随地球一块自转的物体的向心加速度。（3分）
注意：只说明大小关系，但没有给出理由，只得1分

本题难度：简单

5、选择题  发现万有引力定律的物理学家是
[? ]
A．开普勒
B．伽利略 　　
C．牛顿
D．爱因斯坦

参考答案：C

本题解析：

本题难度：简单