1、选择题  如图所示，弹簧秤和细绳重力不计，不计一切摩擦，物体重G=5N，弹簧秤A和B的读数分别为(　　)

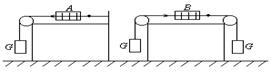
A．5N，0
B．5N，10N
C．5N，5N
D．10N，5N

参考答案：C

本题解析：两图分别对物体分析，物体受重力和绳子的拉力，绳子的拉力等于弹簧的拉力，所以弹簧秤的示数都等于物体的重力，等于5N．故C正确，

本题难度：一般

2、简答题  如图所示，M1N1、M2N2是两根处于同一水平面内的平行导轨，导轨间距离是d=0.5m，导轨左端接有定值电阻R=2Ω，质量为m=0.1kg的滑块垂直于导轨，可在导轨上左右滑动并与导轨有良好的接触，滑动过程中滑块与导轨间的摩擦力恒为f=1N，滑块用绝缘细线与质量为M=0.2kg的重物连接，细线跨过光滑的定滑轮，整个装置放在竖直向上的匀强磁场中，磁场的磁感应强度是B=2T，将滑块由静止释放．设导轨足够长，磁场足够大，M未落地，且不计导轨和滑块的电阻．g=10m/s2，求：
（1）滑块能获得的最大动能
（2）滑块的加速度为a=2m/s2时的速度
（3）设滑块从开始运动到获得最大速度的过程中，电流在电阻R上所做的电功是w=0.8J，求此过程中滑块滑动的距离．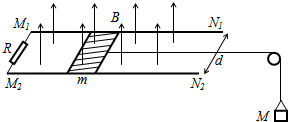

参考答案：（1）滑块匀速运动时，受力平衡，有
Mg=f+BId?①
根据欧姆定律，有
I=ER?②
动生电动势为：
E=BdVm?③
联立①②③解之并代入动能表达式：EK=mVm2?2=0.2J
即滑块能获得的最大动能为0.2J．
（2）对两物体整体受力分析后，运用牛顿第二定律，有
Mg-f-BId=（M+m）a?④
其中
I=ER?⑤
E=BdV?⑥
联立④⑤⑥解之：V=R[(M+m)a]B2d2=0.8m/s
即滑块的加速度为a=2m/s2时的速度为0.8m/s．
（3）对两物体整体运用动能定理，有
Mgx-fx-w=(m+M)Vm22
解得
x=(m+M)[(Mg-f)R]22B4d4+wMg-f=1.4m
即滑块从开始运动到获得最大速度的过程中，滑块滑动的距离为1.4m．

本题解析：

本题难度：一般

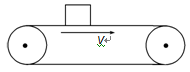
3、选择题  如图，水平传送带以速度v向右匀速传动。现把一个物体无初速度地放在传送带上，这时物体受到的力是

A．重力、弹力
B．重力、弹力、滑动摩擦力
C．重力、滑动摩擦力
D．重力、弹力、静摩擦力

参考答案：B

本题解析：把一个物体无初速度地放在传送带上，物体相对于传送带会向后滑动所以会受到向前的滑动摩擦力，另外物体还受重力和弹力选B

本题难度：简单

4、选择题  细线AO和BO下端系一个物体P，细线长AO＞BO，A．B两个端点在同一水平线上，开始时两线刚好绷直，如图所示。细线的拉力设为FA和FB，保持A．B端点在同一水平线上，使A．B逐渐远离的过程中，关于细线的拉力FA和FB的大小随AB间距离变化的情况是

[　　]
A．FA随距离增大而一直增大
B．FA随距离增大而一直减小
C．FB随距离增大而一直增大
D．FB随距离增大而一直减小

参考答案：A

本题解析：

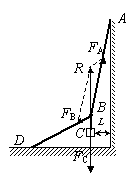
如图：力平行四边形中，当A．B逐渐远离的过程中，R大小一定，TA．TB与R的夹角逐渐增大，力TA一直增大。力TB：开始要减小，角增大到一定程度后，随角增大而增大

本题难度：简单

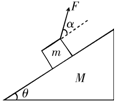
5、简答题  如图所示，质量为M的斜劈倾角为θ，在水平面上保持静止，当将一质量为m的木块放在斜面上时正好匀速下滑．如果用与斜面成α角的力F拉着木块沿斜面匀速上滑．
（1）求拉力F的大小；
（2）若m=1kg，θ=15°，g=10m/s2，求F的最小值以及对应的α的取值．

参考答案：（1）由物体在斜面上恰能匀速下滑，根据共点力平衡条件可得：
mgsinθ=μmgcosθ
解得：μ=tanθ
在拉力F作用下匀速上滑时，受重力、拉力、支持力和摩擦力，如图所示：

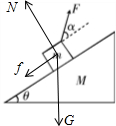
根据共点力平衡条件，有：
平行斜面方向：Fcosα=mgsinθ+f
垂直斜面方向：Fsinα+N=mgcosθ
其中：f=μN
解得：F=mgsin2θcos(θ-α)
（2）若m=1kg，θ=15°，则：
F=mgsin2θcos(θ-α)=mgsin30°cos(15°-α)=mg2cos(15°-α)
当α=15°时，拉力F最小，为12mg=5N
答：（1）拉力F的大小为mgsin2θcos(θ-α)；
（2）F的最小值为5N，对应的α为15°．

本题解析：

本题难度：一般