1、计算题  如图所示，在半径为R的绝缘圆筒内有匀强磁场，方向垂直纸面向里，圆筒正下方有小孔C与平行金属板M、N相通。两板间距离为d，两板与电动势为E的电源连接，一带电量为－q、质量为m的带电粒子（重力忽略不计），在C点正下方紧靠N板的A点，无初速经电场加速后从C点进入磁场，与圆筒发生两次碰撞后从C点射出。已知带电粒子与筒壁的碰撞无电荷量的损失，且碰撞后以原速率返回。求：
(1)筒内磁场的磁感应强度大小；
(2)带电粒子从A点出发至第一次回到A点所经历的时间。

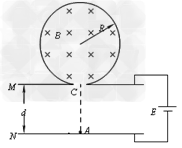
参考答案：解：（1）由题意知，带电粒子从C孔进入，与筒壁碰撞2次再从C孔射出
由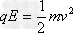
粒子由C孔进入磁场，在磁场中做匀速圆周运动的速率为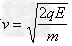
由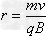，即
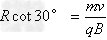
得：?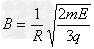
（2）粒子从A到C的加速度为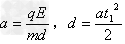
粒子从A到C的时间为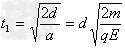
粒子在磁场中运动的时间为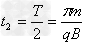
将（1）求得的B值代入，得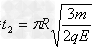
求得：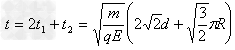

本题解析：

本题难度：一般

2、选择题  如图所示，在光滑绝缘水平面上有一半径为R的圆，AB是一条直径，空间有匀强电场场强大小为E，方向与水平面平行。在圆上A点有一发射器，以相同的动能平行于水平面沿不同方向发射带电量为+q的小球，小球会经过圆周上不同的点，在这些点中，经过C点的小球的动能最大。由于发射时刻不同时，小球间无相互作用。且∠=30°，下列说法正确的是（?）

A．电场的方向与AC间的夹角为30°
B．电场的方向与AC间的夹角为60°
C．小球在A点垂直电场方向发射，恰能落到C点，则初动能为qER
D．小球在A点垂直电场方向发射，恰能落到C点，则初动能为qER

参考答案：AC

本题解析：小球在匀强电场中，从A点运动到C点，根据动能定理qUAC=Ek,因为到达C点时的小球的动能最大，所以UAC最大，即在圆周上找不到与C电势相等的点．且由A到C电场力对小球做正功．过C点作切线，则CF为等势线．过A点作CF的垂线，则该线为电场线，场强方向如图示．

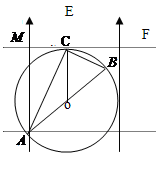
因为∠CAB=30°，所以连接CO，∠ACO=30°，故CO∥AM，所以电场方向与AC间的夹角θ为30°，沿OC方向,选项A正确。小球只受电场力，做类平抛运动．水平方向上：x=Rcos30°=v0t，竖直方向上：y=R+Rsin30°=由以上两式得：Ek=mv2=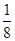qER；选项C正确。

本题难度：一般

3、填空题  如右图所示，水平放置的两平行金属板间距为 d ，电压大小为U，上板中央有孔，在孔正下方的下板表面上有一个质量为 m、、电量为－q的小颗粒，将小颗粒由静止释放，它将从静止被加速，然后冲出小孔，则它能上升的最大高度 h = ______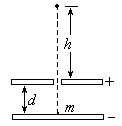

参考答案：

本题解析：从由静止释放到上升到最高点：根据动能定理：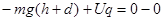
所以上升的最大高度为：h =

本题难度：简单

4、计算题  （12分）质量为m、带电量为+q的小球在O点以初速度并与水平方向成θ角射出，如图所示。不计小球运动过程的阻力，重力加速度为g，试求：

（1）若加上大小一定、方向向左的匀强电场，能保证小球沿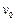方向做直线运动，经过多长时间小球返回O点？
（2）若在某方向加上一定大小的匀强电场后，仍保证小球沿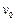方向做直线运动，所加匀强电场场强的最小值是多少？

参考答案：

．解：（1）当匀强电场水平向左，能保证小球沿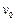方向做直线运动，则重力和电场力的合力与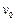方向相反，受力分析如图。?（2分）
小球的加速度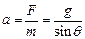：?（2分）
小球返回O点所经历的时间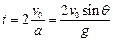：?（2分）
（2）仍保证小球沿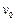方向做直线运动，则重力和电场力的合力与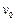在同一直线，做受力分析，当电场力垂直于速度所在的直线时，取得最小值。?（2分）
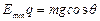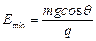由受力分析知，?（2分）
∴?（2分）

本题解析：略

本题难度：一般

5、简答题  如图所示，电容为C、带电量为Q、极板间距为d的电容器固定在绝缘底座上，两板竖直放置，总质量为M，整个装置静止在光滑水平面上。在电容器右板上有一小孔，一质量为m、带电量为+q的弹丸以速度v0从小孔水平射入电容器中（不计弹丸重力，设电容器周围电场强度为0），弹丸最远可到达距右板为x的P点，求：
小题1:弹丸在电容器中受到的电场力的大小；
小题2:x的值；
小题3:当弹丸到达P点时，电容器电容已移动的距离s；
小题4:电容器获得的最大速度。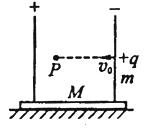

参考答案：
小题1: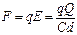
小题2: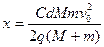
小题3: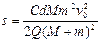
小题4: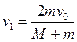

本题解析：
小题1:电容极板电压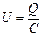?…………①
极板问场强?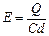?…………②?则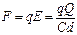?…………③
小题2:弹丸到达P点时两者有共同速度，设为v，由动量守恒有：
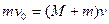?…………④
对弹丸，由动能定理得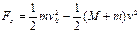：?…………⑤，
解得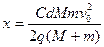?…………⑥
小题3:对电容器，由动能定理得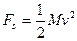：…………⑦
解得?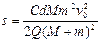?…………⑧
小题4:弹丸最终返回从右板小孔飞出，此时电容器速度最大，设电容器速度为v1、弹丸速度为v2。则由动量守恒有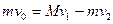：?…………⑨
在整个过程中由能量守恒，即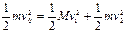?…………⑩
由⑨、⑩两式解得?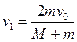?…………11

本题难度：一般