1、计算题 摩天大楼中一部直通高层的客运电梯,行程超过百米。电梯的简化模型如1所示。考虑安全、舒适、省时等因索,电梯的加速度a是随时间t变化的。已知电梯在t = 0时由静止开始上升,a - t图像如图2所示。电梯总质最m = 2.0×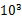 ?kg。忽略一切阻力,重力加速度g取10m/s2。
?kg。忽略一切阻力,重力加速度g取10m/s2。

(1)求电梯在上升过程中受到的最大拉力F1和最小拉力F2;
(2)类比是一种常用的研究方法。对于直线运动,教科书中讲解了由v - t图像求位移的方法。请你借鉴此方法,对比加速度的和速度的定义,根据图2所示a - t图像,求电梯在第1s内的速度改变量△v1和第2s末的速率v2;
(3)求电梯以最大速率上升时,拉力做功的功率p:再求在0~11s时间内,拉力和重力对电梯所做的总功W。
参考答案:(1)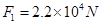 ?
?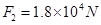
(2)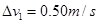 ?
?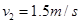
(3)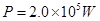 ?
?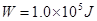
本题解析:解(1)由牛顿第二定律得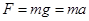
由a-t图像可知,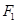 和
和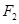 对应的加速度分别为
对应的加速度分别为 ,
,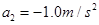
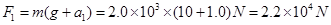
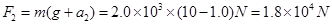
(2)类比可得所求速度变化量等于第1s内a-t图线下的面积
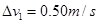
同理可得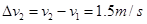
第2s末的速率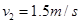
(3)由a-t图像可知,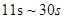 内速率最大,其值等于
内速率最大,其值等于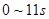 内a-t图线下的面积,
内a-t图线下的面积,
有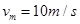
此时电梯做匀速运动,拉力F等重力mg,所求功率
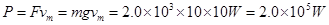
由动能定理得: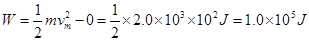
本题难度:一般
2、计算题 一小圆盘静止在桌布上,位于一方桌的水平桌面的中央。桌布的一边与桌的AB边重合,如图。已知盘与桌布间的动摩擦因数为μ1,盘与桌面间的动摩擦因数为μ2。现突然以恒定加速度a将桌布抽离桌面,加速度方向是水平的且垂直于AB边。若圆盘最后未从桌面掉下,则加速度a满足的条件是什么?(以g表示重力加速度)

参考答案:解:设圆盘的质量为m,桌长为l,在桌布从圆盘上抽出的过程中,盘的加速度为a1,有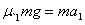 ①
①
桌布抽出后,盘在桌面上作匀减速运动,以a2表示加速度的大小,有 ②
②
设盘刚离开桌布时的速度为v1,移动的距离为x1,离开桌布后在桌面上再运动距离x2后便停下,有 ③,
③,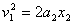 ④
④
盘没有从桌面上掉下的条件是 ⑤
⑤
设桌布从盘下抽出所经历时间为t,在这段时间内桌布移动的距离为x,有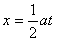 ⑥,
⑥,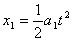 ⑦
⑦
而 ⑧
⑧
由以上各式解得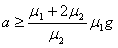 ⑨
⑨
本题解析:
本题难度:困难
3、选择题 在水平面上有a、b两点,相距0.2m,一质点在一恒定的水平合外力作用下沿a向b做直线运动,经过0.2的时间先后通过a、b两点,则该质点通过a、b中点时的速度大小为
A.若力的方向由a向b,则大于1m/s,若力的方向由b向a,则小于1m/s
B.若力的方向由a向b,则小于1m/s,若力的方向由b向a,则大于1m/s
C.无论力的方向如何均小于1m/s
D.无论力的方向如何均大于1m/s
参考答案:D
本题解析:物体做匀变速运动,平均速度小于位移中点速度,平均速度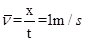 ,所以无论力的方向如何该质点通过a、b中点时的速度均大于1m/s。
,所以无论力的方向如何该质点通过a、b中点时的速度均大于1m/s。
本题难度:一般
4、选择题 质量均为m的A、B两个小球之间系一个质量不计的弹簧,放在光滑的台面上.A紧靠墙壁,如图所示.今用恒力F将B球向左挤压弹簧,达到平衡时,突然将力撤去,此瞬间( )
A.A球的加速度为
B.B球的加速度为
C.A球的加速度为零
D.B球的加速度为
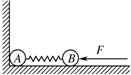
参考答案:力F撤去前弹簧的弹力大小为F.将力F撤去的瞬间,弹簧的弹力没有变化,则A的受力情况没有变化,合力为零,B的合力大小等于F,根据牛顿第二定律得到A球的加速度为零,B球的加速度为a=Fm.所以BC正确,AD错误.
故选:BC
本题解析:
本题难度:一般
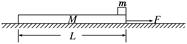
5、计算题 (12分)质量为m=1.0 kg的小滑块(可视为质点)放在质量为M=3.0 kg的长木板的右端,
木板上表面光滑,木板与地面之间的动摩擦因数为μ=0.2,木板长L=1.0 m.开始时两
者都处于静止状态,现对木板施加水平向右的恒力F=12 N,如图19所示,经一段时
间后撤去F.为使小滑块不掉下木板,试求:用水平恒力F作用的最长时间.(g取10 m/s2)
参考答案:1 s
本题解析:撤力前后木板先加速后减速,设加速过程的位移为x1,加速度为a1,加速运动的时间为t1;减速过程的位移为x2,加速度为a2,减速运动的时间为t2.由牛顿第二定律得
撤力前:F-μ(m+M)g=Ma1
解得a1=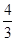 ?m/s2
?m/s2
撤力后:μ(m+M)g=Ma2
解得a2=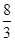 ?m/s2
?m/s2
x1=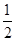 a1t12,x2=
a1t12,x2=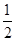 a2t22
a2t22
为使小滑块不从木板上掉下,应满足x1+x2≤L
又a1t1=a2t2
由以上各式可解得t1≤1 s
即作用的最长时间为1 s.
本题难度:一般