1、选择题  固定于竖直面内的粗糙斜杆，在水平方向夹角为300，质量为m的小球套在杆上，在大小不变的拉力作用下，小球沿杆由底端匀速运动到顶端，为使拉力做功最小，拉力F与杆的夹角α和拉力大小F各为多少（　　）
A．α=0°，F=

参考答案：小球由底端到顶端过程由动能定理得W?拉+W?G+W?f=△E?k=0，可知，若要求拉力做功最小应使摩擦力做功W?f为零，即f=0，由f=μF?N得F?N=0，对小球受力分析如图，设拉力方向与杆夹角为α，由平衡条件得F?T．cosα=mgsin30°，F?Tsinα=mgcos30°，两式联立可解得α=60°，F=mg，故D正确，ABC错误．



故选D．

本题解析：

本题难度：一般

2、计算题  (8分)如图，光滑水平面AB与竖直面的半圆形导轨在B点相连接，导轨半径为R，一质量为m的静止木块在A处压缩弹簧，释放后，木块获得一向右的初速度，当它经过B点进入导轨瞬间对导轨的压力是其重力的7倍，之后向上运动恰能通过轨道顶点C，不计空气阻力，试求：

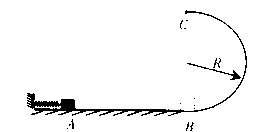
(1)弹簧对木块所做的功；
(2)木块从B到C过程中克服摩擦力做的功；

参考答案：⑴、⑵、

本题解析：本题考查对动能定理的应用，弹簧对物块做功转化为物体的动能，在B点根据合力提供向心力可求出B点动能，即可求出弹簧对木块做功，在C点只有重力提供向心力，可求出C点动能，从B点到C点应用动能定理可求得第二问

本题难度：一般

3、计算题  质量为m的物体以初动能100J从倾角为θ的斜面底端A点沿斜面匀变速滑行到斜面上B点时，物体的动能减少80J，机械能减少32 J，则当物体回到A点时的动能为多少？

参考答案：解：设由A点到B点经过的位移为s1，运动到C点的速度减为0，由B点到C点的位移为?s2
对于由A点到B点的过程运用动能定理可得-mgs1sinθ-μmgcosθs1=-80 J
且μmgcosθs1=32 J
对于由B点到C点的过程运用动能定理可得-mgs2sinθ-μmgcosθs2=-20 J
所以s1=4s2
所以μmgcosθs2=
所以上升过程中摩擦力做的总功为-40 J
下降过程摩擦力大小不变，总位移大小相同，所以下降的过程中摩擦力做功也为-40 J
对全过程利用动能定理即可解得物体回到出发点时的动能为20 J

本题解析：

本题难度：一般

4、计算题  在水平地面MN上方高度为h=0.45m处有一个粗糙绝缘平台PQ，如图所示，平台上方PR右侧有水平向右的有界匀强电场，场强E=1.1×104N/C。有一质量m=1.0×10-3kg、带电量为q=-1.0×10-6C的滑块放在平台上，距离平台左端P点L=0.5m处，滑块与平台的滑动摩擦因数为μ=0.2。现给滑块水平向左的初速度v0=4m/s，问：
（1）滑块经过P点时的速度多大？
（2）滑块落地点距N点多远？

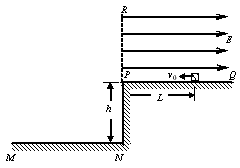
参考答案：解：（1）由动能定理：
得：
（2）由，得

本题解析：

本题难度：一般

5、简答题  如图所示，长木板A上右端有一物块B，它们一起在光滑的水平面上向左做匀速运动，速度
v0=2.0m/s．木板左侧有一个与木板A等高的固定物体c．已知长木板A的质量为mA=1.0kg，物块B的质量为mB=3.0kg，物块B与木板A间的动摩擦因数μ=0.5，取g=10m/s2．

（1）若木板A足够长，A与C第一次碰撞后，A立即与C粘在一起，求物块曰在木板A上滑行的距离工应是多少；
（2）若木板A足够长，A与C发生碰撞后弹回（碰撞时间极短，没有机械能损失），求第一次碰撞后A、B具有共同运动的速度；
（3）若木板A长为0.51m，且A与C每次碰撞均无机械能损失，求A与C碰撞几次，B可脱离A？

参考答案：（1）A与C碰撞后速度变为0，而B继续运动，受摩擦力作用速度由V0减到0，由动能定理得：
? ?-μmBgL=0-12mB?V02
? ?得? L=0.40m?
? （2）若A与C碰撞后速度仍为V0，方向相反；以AB为研究对象，设公共速度v，
? 水平方向不受外力动量守恒，设向左为正方向：
? mBV0-mAV0=（mA+mB）v?
? 代入数据得v=1.0m/s，方向水平向左．?
? （3）第一次A与C碰撞后，A、B有共同的速度V′，B相对A滑行的距离L1，则：
? μmAg?L1=12mAV02+?12mBV02-12(mA+mB)?V′2
?代入数据得L1=0.40m；
?第二次A、C碰撞后至AB有公共速度V′′，B在A上滑行L2，则：
? mBv′-mAv′=（mA+mB）V′′
?μmAg?L2=12mAV′2+?12mBV′2-12(mA+mB)?v′′2
?得L2=0.10m
? 设第三次AC碰撞后，AB有公共速度V′′′，B在A上滑行L3，则：
? mBV′′-mAV′′=（mA+mB）V′′′
? μmAgL3=12mAV′′2+?12mBV′′2-12(mA+mB)V′′′2
? 代入数据得L3=0.025m
?由L1+L2+L30.525m＞0.51m? 得第三次碰撞后B可脱离A．
答：（1）物块B在木板A上滑行的距离 0.4m
? （2）第一次碰撞后A、B具有共同运动的速度1.0m/s，方向水平向左．
? （3）A与C碰撞3次．

本题解析：

本题难度：一般