1、简答题 有一个固定竖直放置的圆形轨道,半径为R,由左右两部分组成.如图所示,右半部分AEB是光滑的,左半部分BFA是粗糙的.现在最低点A给一质量为M的小球一个水平向右的初速度,使小球沿轨道恰好运动到最高点B,小球在B点又能沿BFA回到A点,到达A点时对轨道的压力为4mg.
?(1)在求小球在A点的速度v0时,甲同学的解法是:由于小球恰好到达B点,故在B点小球的速度为零,
m=2mgR,所以v0=2.
(2)在求小球由BFA回到A点的速度时,乙同学的解法是:由于回到A点时对轨道的压力为4mg,故4mg=,所以vA=2.?你同意两位同学的解法吗?如果同意请说明理由;若不同意,请指出他们的错误之处,并求出结果.
(3)根据题中所描绘的物理过程,求小球由B经F回到A的过程中克服摩擦力所做的功.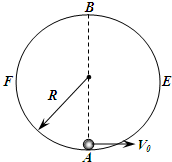
参考答案:不同意,两位同学的解法都错误,甲同学认为最高点的临界速度为零,实际上在最高点的临界情况是弹力为零,靠重力提供向心力,有最小速度.乙同学认为在最低点是支持力提供向心力,实际上时竖直方向上的合力提供向心力.
(1)小球恰好到达B点,在B点小球的速度不为零.
小球由AEB到B点的速度时mg=mvB2R,vB=
本题解析:
本题难度:一般
2、选择题 物体在恒定的合力F作用下做直线运动,在时间 内速度由0增大到
内速度由0增大到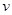 ,在时间
,在时间 内速度由
内速度由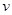 增大到
增大到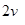 。设F在
。设F在 内做的功是
内做的功是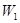 ,冲量是
,冲量是 ;在
;在 内做的功是
内做的功是 ,冲量是
,冲量是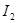 ;那么?(?)
;那么?(?)
A.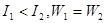
B.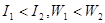
C.
D.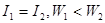
参考答案:D
本题解析: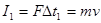 ,
, ,所以冲量相同,由动能定理
,所以冲量相同,由动能定理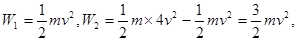 所以
所以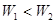
本题难度:简单
3、简答题 如图所示,可视为质点的三物块A、B、C放在倾角为30°、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=
,A与B紧靠在一起,C紧靠在固定挡板上,三物块的质量分别为mA=0.80kg、mB=0.64kg、mC=0.50kg,其中A不带电,B、C的带电量分别为qB=+4.0×10-5C、qC=+2.0×10-5C且保持不变,开始时三个物块均能保持静止且与斜面间均无摩擦力作用.如果选定两点电荷在相距无穷远处的电势能为0,则相距为r时,两点电荷具有的电势能可表示为Ep=k.现给A施加一平行于斜面向上的拉力F,使A在斜面上作加速度a=1.5m/s2的匀加速直线运动,经过时间t0,拉力F变为恒力,当A运动到斜面顶端时撤去拉力F.已知静电力常量k=9.0×109N-m2/C2,g=10m/s2.求:
(1)未施加拉力F时物块B、C间的距离;
(2)t0时间内A上滑的距离及库仑力做的功;
(3)拉力F对A物块做的总功.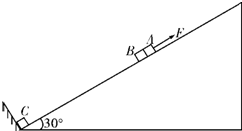
参考答案:(1)A、B、C处于静止状态时,设B、C间距离为L1,则C对B的库仑斥力:F0=kqCqBL21?
以A、B为研究对象,根据力的平衡?F0=(mA+mB)gsin30°?
联立解得?L1=1.0m?
(2)给A施加力F后,A、B沿斜面向上做匀加速直线运动,C对B的库仑斥力逐渐减小,A、B之间的弹力也逐渐减小.经过时间t0,B、C间距离设为L2,A、B两者间弹力减小到零,此后两者分离,力F变为恒力.则t0时刻C对B的库仑斥力为:F0=kqCqBL22?①
以B为研究对象,由牛顿第二定律有:F0-mBgsin30°-μmBgcos30°=mBa?②
联立①②解得?L2=1.2m?
则t0时间内A上滑的距离△L=L2+L1=0.2m?
设t0时间内库仑力做的功为W0,由功能关系有
W0=kq1q2L1-kq1q2L2
代入数据解得?W0=1.2J? ③
(3)设在t0时间内,末速度为v1,力F对A物块做的功为W1,由动能定理有
W1+W2+WG+Wf=12(mA+mB)v21? ④
而?Wf=-μ(mA+mB)g?△Lcos30°,WG=-(mA+mB)g△Lsin30°⑤
v21=2a△L?⑥
由③~⑦式解得?W1=1.05J? ⑦
经过时间t0后,A、B分离,力F变为恒力,对A由牛顿第二定律有
F-mAgsin30°-μmAgcos30°=mAa? ⑧
力F对A物块做的功?W2=F?(L-L2)? ⑨
由⑧⑨式代入数据得?W2=5?J?
则力F对A物块做的功:W=W1+W2=6.05J?
答:(1)未施加拉力F时物块B、C间的距离1.0m;
(2)t0时间内A上滑的距离及库仑力做的功1.2J;
(3)拉力F对A物块做的总功是6.05J.
本题解析:
本题难度:一般
4、简答题 如图所示,虚线上方有方向竖直向下的匀强电场,虚线上下有相同的匀强磁场,磁感应强度为B,方向垂直纸面向外,ab是一根长为l的绝缘细杆,沿电场线放置在虚线上方,b端恰在虚线上,将一套在杆上的带电量为q、质量为m的小环(小环重力忽略不计),从a端由静止释放后,小环先作加速运动,后作匀速运动到达b端,已知小环与绝缘杆间的动摩擦系数为μ,当小环脱离杆进入虚线下方后,运动轨迹是半圆,圆的半径是
,求:
(1)小环到达b点的速度vb;
(2)匀强电场的场强E.
参考答案:
(1)小环在磁场中做匀速圆周运动,由洛仑兹力提供向心力:
qvbB=mv2bR?
又因R=?l3
解得b点速度为:vb=Bql3m
(2)小环在沿杆向下运动时,受力情况如图所示:
当小环在杆上做匀速运动时由平衡条件得
在水平方向有:N=qvbB? (1)
在竖直方向有:qE=f ? (2)
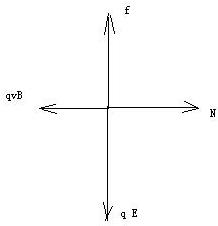
又因摩擦力:f=μN (3)
由(1)(2)(3)式解得,匀强电场的场强E为:E=B2ql3μm
答:(1)小环到达b点的速度Bql3m;
(2)匀强电场的场强B2ql3μm.
本题解析:
本题难度:一般
5、选择题 如图所示是一个盆式容器,盆内侧壁与盆底BC的连接处是一段与BC相切的圆弧,B,C点为水平的, 其距离d=0. 50m。盆边缘的高度h=0. 30m。在A处放一个质量为m的小物块并让其从静止开始下滑,已知盆内侧壁是光滑的,而盆底BC面与小物块间的动摩擦因数μ=0.10。小物块在盆内来回滑动, 最后停下来,则所停地点到B处的距离为

[? ]
A. 0. 50m
B. 0. 25m
C. 0. 10m
D. 0
参考答案:D
本题解析:
本题难度:一般