1、计算题 如图所示,质量为m=0.2kg的小球(可视为质点)从水平桌面左端点A以初速度v0水平抛出,桌面右侧有一竖直放置的光滑轨道MNP,其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧,MN为其竖直直径。P点到桌面的竖直距离也为R。,g=10m/s2,小球飞离桌面后恰由P点无碰撞地落入圆轨道
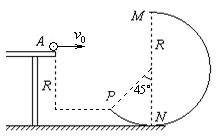
求:(1)小球在A点的初速度v0及AP间水平距离x;
(2)小球到达圆轨道最低点N时对N点的压力;
(3)判断小球能否到达圆轨道最高点M。
参考答案:(1)物块由A点做平抛运动,在P点恰好沿圆轨道的切线进入轨道,则物块在P点的竖直分速度为 ?v0
?v0
由平抛运动规律得,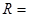
 ,x= v0t
,x= v0t
解得v0 =" 4" m/s , x=1.6m.?(4分)
(2)物块在P点的速度为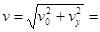 4
4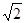 ?m/s
?m/s
物块从P点到N点,由动能定理得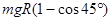
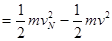
物块在N点,由牛顿第二定律得
解得物块所受支持力 9.17N
9.17N
由牛顿第三定律得,物块对N点的压力为 9.17 N,方向竖直向下。(4分)
9.17 N,方向竖直向下。(4分)
(3)假设小球能够到达M点,由动能定理得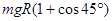
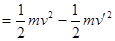
解得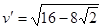 m/s
m/s
小球能够完成圆周运动,在M点须有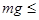
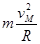 ,即
,即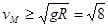 m/s,由
m/s,由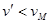 知,小球不能到达圆轨道最高点M。(4分)
知,小球不能到达圆轨道最高点M。(4分)
本题解析:本题是高中里面比较重要的基础知识点。考察同学们对平抛运动,圆周运动、机械能守恒定律以及是否能过圆轨道最高点的条件。通过巧妙的设计将这些知识点衔接起来。题目中“小球飞离桌面后恰由P点无碰撞地落入圆轨道”则说明平抛运动该轨迹的瞬时速度方向正好为P点切线方向。作为切入口,利用分解知识从而。打开解题思路。
考点分析:本题结合了平抛运动,向心力知识,巧妙的将平抛运动某处的瞬时速度与圆弧轨道相接;利用机械能守恒定律,求最低点速度;利用向心力知识,即可求出最低处所受支持力;利用牛顿第三定律将其转化为对轨道压力。根据动能定理,可以求出起到最高点的速度,并利用小球经过圆轨道上最高点的条件,即可判断出小球是否可以最高点。
总结评价:本题是属于各个知识点虽然都简单,但是在物理学上的地位都很重要的题型。经过巧妙的设计和衔接将各个基础且重要的问题有机集成在一个题目当中,不愧是经典的题型。不管是老师还是学生应该对这类问题好好总结,从中找到解决这些知识点的方法,以提高学习效率。
本题难度:一般
2、简答题 水平路面上有一质量是30kg的手推车,在受到60N的水平推力时做加速度为1.5m/s2的匀加速运动.如果撤去推力,车的加速度是多少?
参考答案:根据牛顿第二定律得,F-f=ma,解得f=F-ma=60-30×1.5N=15N,撤去拉力后,加速度:a′=fm=1530m/s2=0.5m/s2,方向与推力方向相反.
答:车的加速度是0.5m/s2,方向与推力方向相反
本题解析:
本题难度:一般
3、计算题 如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,杆和球在竖直面内转动,已知球B运动到最高点时,球B对杆恰好无作用力.
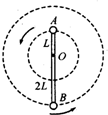
求:(1)球B在最高点时,杆对水平轴的作用力大小.
(2)球B转到最低点时,球B的速度是多大?
参考答案:(1)1. 5 mg.(2)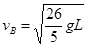
本题解析:(1)球B在最高点时速度为v0,有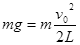 ,
,
得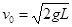 .
.
此时球A的速度为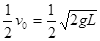 ,
,
设此时杆对球A的作用力为FA,则
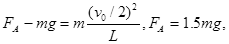
A球对杆的作用力为 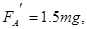
水平轴对杆的作用力与A球对杆的作用力平衡,再据牛顿第三定律知,杆对水平轴的作用力大小为
F0="1." 5 mg.
(2)设球B在最低点时的速度为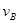 ,取O点为参考平面,据机械能守恒定律有
,取O点为参考平面,据机械能守恒定律有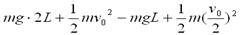
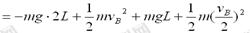 ?
?
解得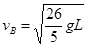
本题难度:一般
4、填空题 如右图所示,质量之比2:1的球A、B,由轻质弹簧相连后再用细线悬挂在正在竖直向上做匀速运动的电梯内,细线承受的拉力为F;某时刻突然剪断细线,那么在细线断的瞬间,弹簧的弹力大小为___________;小球A的加速度大小为_________
参考答案:0.33F?,? 1.5g
本题解析:由于弹簧形变量较大,在间断细线的瞬间弹簧弹力不能发生突变,在匀速运动阶段F=3mg,kx=2mg,kx=0.33F,小球A受到竖直向下的重力2mg和竖直向下的弹簧弹力mg的作用,所以加速度为1.5g
点评:难度较小,明确模型的类型,如果是细绳,则弹力可以突变,如果是弹簧或橡皮筋则弹力不能突变
本题难度:简单
5、选择题 在水平的足够长的固定木板上,一小物块以某一初速度开始滑动,经一段时间t后停止。现将该木板改置成倾角为45°的斜面,让小物块以相同的初速度沿木板上滑。若小物块与木板之间的动摩擦因数为μ。则小物块上滑到最高位置所需时间与t之比为
[? ]
A.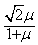
B.
C.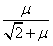
D.
参考答案:A
本题解析:
本题难度:一般
It is never too late to learn. 学习从不嫌晚.