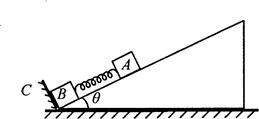
1、选择题 在倾角为θ的光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量均为m,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一恒力F沿斜面方向拉物块A使之向上运动,当物块B刚要离开C时,A的速度为v,则此过程(弹簧的弹性势能与弹簧的伸长量或压缩量的平方成正比,重力加速度为g)
A.物块A运动的距离为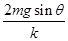
B.物块A加速度为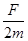
C.拉力F做的功为
D.拉力F对A做的功等于A的机械能的增加量
参考答案:AD
本题解析:初始时刻以A为研究对象分析受力可知弹簧弹力 ,故可知此时弹簧的压缩量为
,故可知此时弹簧的压缩量为 ,同理,当物体B刚要离开C时,以物体B为研究对象分析受力可知弹簧弹力
,同理,当物体B刚要离开C时,以物体B为研究对象分析受力可知弹簧弹力 ,此时弹簧的伸长量为
,此时弹簧的伸长量为 ,所以可知物体A运动的距离
,所以可知物体A运动的距离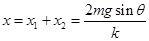 ,故选项A正确;此时再以物体A研究对象分析受力有
,故选项A正确;此时再以物体A研究对象分析受力有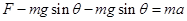 ,故其加速度为
,故其加速度为 ,所以选项B错误;对系统初末状态而言,弹簧的弹性势能没有改变,由动能定理可知
,所以选项B错误;对系统初末状态而言,弹簧的弹性势能没有改变,由动能定理可知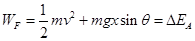 ,所以选项C错误、D正确;
,所以选项C错误、D正确;
本题难度:一般
2、计算题 如图所示,一水平传送带始终保持着大小为v=4m/s的速度做匀速运动。在传送带右侧有一半圆弧形的竖直放置的光滑圆弧轨道,其半径为R=0.2m,半圆弧形轨道最低点与传送带右端B衔接并相切,一小物块无初速地放到皮带左端A处,经传送带和竖直圆弧轨道至最高点C。已知当A、B之间距离为s=1m时,物块至最高点对轨道的压力为零,(g=10m/s2)则:
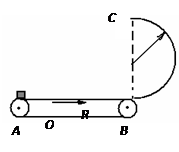
(1)物块至最高点C的速度为多少?
(2)物块在B点的速度为多少?物块与皮带间的动摩擦因数为多少?
(3)若只改变传送带的长度,使滑块滑至圆弧轨道的最高点C时对轨道的压力最大,传送带的长度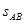 应满足什么条件?
应满足什么条件?
参考答案:(1)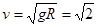 m/s(2)
m/s(2) (3)
(3) ≥1.6 m
≥1.6 m
本题解析:(1)设小物块质量为m,至最高点C的速度为v?
 ?(2分)?
?(2分)?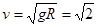 m/s(2分)
m/s(2分)
(2)从B到C过程中,
 ?(2分)
?(2分) ?m /s(2分)
?m /s(2分)
从A到B的过程中
 ?(2分)?
?(2分)? (2分)
(2分)
(3)设刚好到达B点的最大速度为4 m /s(1分)
设AB之间的长度为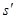
 ?(1分)?
?(1分)? m
m
 ≥1.6 m(1分)
≥1.6 m(1分)
本题考查圆周运动规律,在最高点由重力提供向心力,列式求解,从B到C过程中,由动能定理可求出B点速度,再由传送带的摩擦力做功求得动摩擦因数
本题难度:一般
3、计算题 (12分)如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10 27kg,电荷量q = 3.2×10 19C,初速度v = 3.2×106m/s。(sin37°= 0.6,cos37°= 0.8)求:

(1)α粒子在磁场中作圆周运动的轨道半径R;
(2)金箔cd被α粒子射中区域的长度L;
(3)设打在金箔上d端离cd中心最远的α粒子穿出金箔进入电场,在电场中运动通过N点,SN⊥ab且SN = 40cm,则此α粒子从金箔上穿出时,损失的动能△EK为多少?
参考答案:(1)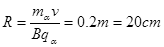 ?(2)
?(2) ?
?
(3)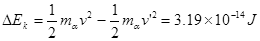
本题解析:(1)α粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,即  ?(1分)
?(1分)
则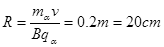 ?(2分)
?(2分)
(2)设cd中心为O,向c端偏转的α粒子,当圆周轨迹与cd相切时偏离O最远,设切点为P,对应圆心O1,如图所示,则由几何关系得:
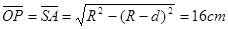 ?(1分)
?(1分)
向d端偏转的α粒子,当沿sb方向射入时,偏离O最远,设此时圆周轨迹与cd交于Q点,对应圆心O2,如图所示,则由几何关系得:
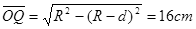 ?(1分)
?(1分)

故金箔cd被α粒子射中区域的长度 ?(1分)
?(1分)
(3)设从Q点穿出的α粒子的速度为v′,因半径O2Q∥场强E,则v′⊥E,故穿出的α粒子在电场中做类平抛运动,轨迹如图所示。?
沿速度v′方向做匀速直线运动,?位移 ?(1分)
?(1分)
沿场强E方向做匀加速直线运动,位移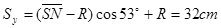 ?(1分)
?(1分)
则由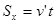 ?
?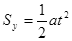 ?
?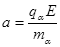 ?得:
?得:  ?(2分)
?(2分)
故此α粒子从金箔上穿出时,损失的动能为
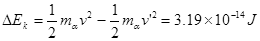 (2分)
(2分)
本题难度:一般
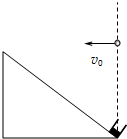
4、简答题 如图,倾角为θ的粗糙斜面的底端有一凹形小滑块,在底端竖直线上离底端高度为H处有一个小球,小球以一定的水平速度v0抛出.
(1)要使小球垂直打在斜面上,试推导小球离斜面底端的高度H与小球速度v0之间的关系.
(2)若斜面倾角θ=37°,凹形小滑块的质量m=1kg,小滑块与斜面间的动摩擦因数μ=0.25.现小滑块以某一初速度从斜面底端上滑,同时在斜面底端正上方的小球以初速度3m/s水平抛出,经过一段时间,小球恰好垂直斜面方向落入凹槽,此时,小滑块还在上滑过程中.求小滑块运动的时间和小滑块的动能变化量.(已知sin37°=0.6,cos37°=0.8,g取10m/s2)
参考答案:(1)小球做平抛运动:
v0=vytanθ,vy=gt,
小球下落的高度:h1=12gt2,
小球的水平位移:x=v0t,
小球的落点到斜面底端的竖直高度:h2=xtanθ,
综上可得,小球抛出点到斜面底端的竖直高度:
H=h1+h2=v022g(2+cot2θ);
(2)小滑块运动的时间与小球的时间相同:
t=v0gtanθ=0.4s,
滑块运动的位移:s=xcosθ=1.5m,
滑块受到的合外力:F=mgsinθ+μmgcosθ=8N,
根据动能定理可得滑块的动能变化量为:△EK=-Fs=-12J;
答:(1)小球离斜面底端的高度H与小球速度v0之间的关系为H=h1+h2=v022g(2+cot2θ);
(2)小滑块运动的时间为0.4s,小滑块的动能变化量为-12J.
本题解析:
本题难度:一般
5、计算题 如图所示,在竖直平面内固定着半径为R的半圆形轨道,小球B静止在轨道的最低点,小球A从轨道右端正上方3.5R处由静止自由落下,沿圆弧切线进入轨道后,与小球B发生弹性碰撞。碰撞后B球上升的最高点C,圆心O与C的连线与竖直方向的夹角为60°。若两球均可视为质点,不计一切摩擦,求A、B两球的质量之比mA:mB。
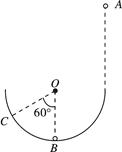
参考答案:1:5
本题解析:小球A从高处静止下落至轨道的最低点,由机械能守恒定律
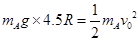 ?
?
小球A与小球B发生弹性碰撞,由动量守恒定律和能量守恒定律
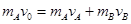 ?
?
 ?
?
B球上升到最高点C,由机械能守恒定律
 ?
?
联立解得
本题难度:一般