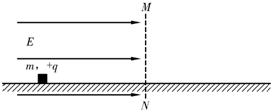
1、填空题  如图所示，质量为m、电荷量为+q的滑块，静止在绝缘水平面上．某时刻，在MN的左侧加一个场强为E的匀强电场，滑块在电场力的作用下开始向右运动．已知滑块与MN之间的距离为d，滑块与水平面间的动摩擦因数为μ，重力加速度为g．求：
（1）滑块在电场中运动时加速度a的大小；
（2）滑块停止时与MN间的距离x．

参考答案：（1）根据牛顿第二定律有：
qE-f=ma
mg-N=0
又因为：f=μN
所以有：a=qE-μmgm
（2）小物块在整个运动过程中，根据动能定理有：
（qE-μmg）d-μmgx=0-0
所以：x=(qE-μmg)dμmg
答：（1）滑块在电场中运动时加速度a的大小为qE-μmgm；
（2）滑块停止时与MN间的距离x=(qE-μmg)dμmg

本题解析：

本题难度：简单

2、计算题  科技馆中，有一个模拟万有引力的装置。在如图1所示的类似锥形漏斗固定的容器中，有两个小球在该容器表面上绕漏斗中心轴做水平圆周运动，其运行能形象地模拟了太阳系中星球围绕太阳的运行。图2为示意图，图3为其模拟的太阳系运行图。图2中离中心轴的距离相当于行星离太阳的距离。

（1）在图3中，设行星A1和B1离太阳距离分别为r1和r2，求A1和B1运行速度大小之比。
（2）在图2中，若质量为m的A球速度大小为v，在距离中心轴为x1的轨道面上旋转，由于受到微小的摩擦阻力，A球绕轴旋转同时缓慢落向漏斗中心。当其运动到距离中心轴为x2的轨道面时，两轨道面之间的高度差为H。求此过程中A球克服摩擦阻力所做的功。

参考答案：（1）（2）

本题解析：（1）设A1和B2的质量分别为m1和m2，
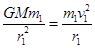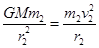根据万有引力定律和牛顿运动定律：?①??②）3分
由①②得 ?③1分
（2)设小球距离中心轴x2的轨道面速度为v′,由于小球模拟行星运动，则有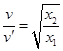：?④1分
由动能定理： ?⑤，2分?解得：⑥1分
点评：解决本题的关键掌握万有引力公式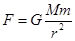，以及会通过动能定理求解复杂过程中功能的变化．

本题难度：一般

3、选择题  如图甲所示，静置于光滑水平面上坐标原点处的小物块，在水平拉力F作用下，沿x轴方向运动，拉力F随物块所在位置坐标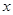的变化关系如图乙所示，图线为半圆。则小物块运动到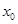处时的动能为(　　)

A．
B．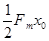
C．
D．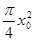

参考答案：C

本题解析：根据F-x图像的面积的含义代表其做功，且因为动能定理，合外力做功等于其动能改变量，即末状态的动能大小等于合外力做功即面积大小
点评：本题考查了动能定理的含义及其理解，通过F-x图像得到总功的表达式。

本题难度：简单

4、选择题  如图所示,空间有一水平方向的匀强电场,一带电微粒以一定初速度从A点沿直线运动到B点，微粒除受到电场力和重力外，不再受其它力，则此过程微粒(? )

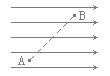
A．电势能增加
B．电势能减小
C．动能增加
D．动能不变

参考答案：A

本题解析：

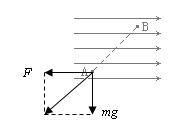
如图所示，微粒受到电场力和重力，它们的合力方向一定与AB在同一条直线上，斜向左下方，微粒运动过程中，电场力做负功，电势能增加，A选项正确，B选项错误；由动能定理，合外力做负功，动能减小，故C、D选项错误。

本题难度：一般

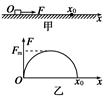
5、计算题  一个质量为m，带有电荷-q的小物块，可在水平轨道OX上运动，O端有一与轨道垂直的固定墙，轨道处于匀强电场中，场强大小为E，方向沿OX轴正方向，如图所示，小物体以初速v0从离O点为x0处沿OX轨道运动，运动时受到大小不变的摩擦力f作用，且f＜qE。设小物体与墙碰撞时不损失机械能且电量保持不变。求它在停止运动前所通过的总路程s。

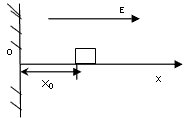
参考答案：解：设小物块从开始运动到停止在O处的往复运动过程中位移为x0，往返路程为s。根据动能定理有

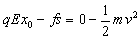
解得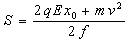

本题解析：

本题难度：一般